Question

Find the value of $\sec \left( 90-\theta \right)=$

A) $\cos ec\theta $
B) $\sin \theta $
C) $\cos \theta $
D) $\text{None of these}$

Answer 1

Hint: Apply trigonometric ratios for $\angle A$ and $\angle B$ to see the relation.
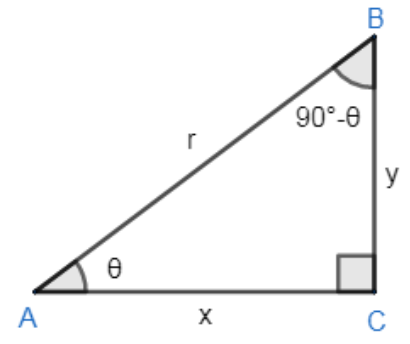
For $\angle A$ -
$\angle A=\theta $
Perpendicular = BC = y.
Base = AC = x.
Hypotenuse = AB = r.
For $\angle B$ -
$\angle B=90-\theta $
Perpendicular = AC = x
Base = BC = y
Hypotenuse = AB = r.

Complete step by step solution:
In a right triangle, the side opposite to the right angle is called hypotenuse. And ‘perpendicular’ and ‘base’ are different for the two angles. The side opposite to the angle (If the angle is other than the right angle) is called its perpendicular side and the remaining one other that perpendicular and hypotenuse is called its ‘base’ side.
In question it is asked to find. $\sec \left( 90-\theta \right)$
We know that $\sec \theta =\dfrac{1}{\cos \theta }$ .
$\therefore \sec \left( 90-\theta \right)=\dfrac{1}{\cos \left( 90-\theta \right)}$ .
And $\cos \left( 90-\theta \right)=\dfrac{\text{Base}}{\text{hypotenuse}}$ .
We know –
$\angle B=90-\theta $ .
For $\angle B$ , base = BC = y and hypotenuse = AB = r.
So, $\cos \left( 90-\theta \right)=\cos B=\dfrac{y}{r}$ .
And $\sec \left( 90-\theta \right)=\dfrac{1}{\cos \left( 90-\theta \right)}$ .
$\Rightarrow \sec \left( 90-\theta \right)=\dfrac{r}{y}$ …………………………… (1)
We know that –
$Y=BC$
And BC = perpendicular side of $\angle A$ .
So,
$\begin{align}
  & \sin \theta =\sin A=\dfrac{BC}{BA} \\
 & \Rightarrow \sin \theta =\dfrac{y}{r} \\
 & \Rightarrow \dfrac{1}{\sin \theta }=\dfrac{r}{y} \\
\end{align}$
And we know that $\cos \theta =\dfrac{1}{\sin \theta }$ .
$\Rightarrow \cos ec\theta =\dfrac{r}{y}$ ……………………….. (2)
From equation (1) and (2) –
$\sec \left( 90-\theta \right)=\cos ec \theta $ .
Hence, option (a) is the correct answer.

Note: A student should memorize the relations between trigonometric ratio of $\theta $ and $90-\theta $. These relations are used for solving many questions. If we had recollected the relation $\sec \left( 90-\theta \right)=\text{cosec}\theta $ , then we could have easily solved this question without converting to cosine terms and then deducing the results. We must keep this point in mind that whenever the relation is 90 plus or minus $\theta $ , then the function changes. So, for sine it will be cosine, for tangent it will be cotangent and for secant it will be cosecant and vice versa. The sign of the function depends on the quadrant the function falls in.