
Find the value of p(0), p(1) and p(2) where p(x) is given by
$p\left( x \right)={{x}^{3}}$
Answer
587.7k+ views
Hint: p(a) can be calculated by substituting x = a in the expression of p(x). Hence substitute x = 0, 1, 2 successively in the expression of p(x) to get the value of p(0), p(1) and p(2) respectively.
Complete step-by-step answer:
Alternatively, use synthetic division to get the value of p(0), p(1) and p(2).
Calculating p(0):
We have $p\left( x \right)={{x}^{3}}$
Substituting x= 0 in the expression of p(x), we get
$p\left( 0 \right)={{0}^{3}}=0$
Hence, we have p(0) = 0.
Calculating p(1):
We have $p\left( x \right)={{x}^{3}}$
Substituting x= 1 in the expression of p(x), we get
$p\left( 1 \right)={{\left( 1 \right)}^{3}}=1$
Hence, we have p(1) = 1.
Calculating p(2):
We have $p\left( x \right)={{x}^{3}}$
Substituting x=2 in the expression of p(x), we get
$p\left( 2 \right)={{\left( 2 \right)}^{3}}=8$
Hence, we have p(2) = 8.
Note: Alternative method: Synthetic division: Best method.
In this method, we start by writing coefficients of the polynomial in order from the highest degree to the constant term. If in between some degree terms are missing we set their coefficient as 0.
Hence $p\left( x \right)={{x}^{3}}={{x}^{3}}+0{{x}^{2}}+0x+0$ will be written as

Now each the point which has to be substituted(say x= 0) is written as follows
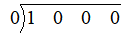
0 is placed below the first term

Since the last carrydown is 0, we have $p\left( 0 \right)=0$.
For x =1:

Since the last carrydown is 1, we have $p\left( 1 \right)=1$
For x = 2:
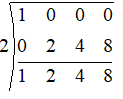
Since the last carrydown is 8, we have $p\left( 2 \right)=8$
Complete step-by-step answer:
Alternatively, use synthetic division to get the value of p(0), p(1) and p(2).
Calculating p(0):
We have $p\left( x \right)={{x}^{3}}$
Substituting x= 0 in the expression of p(x), we get
$p\left( 0 \right)={{0}^{3}}=0$
Hence, we have p(0) = 0.
Calculating p(1):
We have $p\left( x \right)={{x}^{3}}$
Substituting x= 1 in the expression of p(x), we get
$p\left( 1 \right)={{\left( 1 \right)}^{3}}=1$
Hence, we have p(1) = 1.
Calculating p(2):
We have $p\left( x \right)={{x}^{3}}$
Substituting x=2 in the expression of p(x), we get
$p\left( 2 \right)={{\left( 2 \right)}^{3}}=8$
Hence, we have p(2) = 8.
Note: Alternative method: Synthetic division: Best method.
In this method, we start by writing coefficients of the polynomial in order from the highest degree to the constant term. If in between some degree terms are missing we set their coefficient as 0.
Hence $p\left( x \right)={{x}^{3}}={{x}^{3}}+0{{x}^{2}}+0x+0$ will be written as

Now each the point which has to be substituted(say x= 0) is written as follows
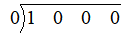
0 is placed below the first term

Since the last carrydown is 0, we have $p\left( 0 \right)=0$.
For x =1:

Since the last carrydown is 1, we have $p\left( 1 \right)=1$
For x = 2:

Since the last carrydown is 8, we have $p\left( 2 \right)=8$
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




