
Find the value of other five trigonometric ratios:
$\sec x = \dfrac{{13}}{5}$ , x lies in the fourth quadrant.
Answer
590.7k+ views
Hint: Given that x lies in fourth quadrant. Now if x lies in the fourth quadrant, only \[\cos x\] and \[\sec x\] is positive.
Also, note the following important formulae:
$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
${\sin ^2}x + {\cos ^2}x = 1$
\[{\sec ^2}x - {\tan ^2}x = 1\]
\[{\operatorname{cosec} ^2}x - {\cot ^2}x = 1\]
Now, the value of \[\sec x\] is given. Therefore find the value of the other five trigonometric ratios with the help of aforementioned formulae.
Complete step-by-step answer:
Given, $\sec x = \dfrac{{13}}{5}$
Therefore $\cos x = \dfrac{1}{{\sec x}} = \dfrac{5}{{13}}$
Now,
${\sin ^2}x + {\cos ^2}x = 1$
$ \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x$
Taking square root we get,
$ \Rightarrow \sin x = \pm \sqrt {1 - {{\cos }^2}x} $
On substituting the value of \[\cos x\] we get,
$ \Rightarrow \sin x = \pm \sqrt {1 - {{\left( {\dfrac{5}{{13}}} \right)}^2}} $
On simplification we get,
$ \Rightarrow \sin x = \pm \sqrt {1 - \dfrac{{25}}{{169}}} = \pm \sqrt {\dfrac{{144}}{{169}}} $
As, x lies in the fourth quadrant, so value of \[\sin x\] will be negative,
$ \Rightarrow \sin x = - \dfrac{{12}}{{13}}{\text{, }}$
Therefore, $\operatorname{cosecx} = \dfrac{1}{{\sin x}} = - \dfrac{{13}}{{12}}$
Again,
\[\because {\sec ^2}x - {\tan ^2}x = 1\]
\[ \Rightarrow {\tan ^2}x = {\sec ^2}x - 1\]
On taking square root we get,
\[ \Rightarrow \tan x = \pm \sqrt {{{\sec }^2}x - 1} \]
On substituting the value of \[\sec x\] we get,
\[ \Rightarrow \tan x = \pm \sqrt {{{\left( {\dfrac{{13}}{5}} \right)}^2} - 1} \]
On simplification we get,
\[ \Rightarrow \tan x = \pm \sqrt {\dfrac{{169}}{{25}} - 1} = \pm \sqrt {\dfrac{{144}}{{25}}} \]
As, x lies in the fourth quadrant, so value of \[\tan x\] will be negative,
\[ \Rightarrow \tan x = - \dfrac{{12}}{5}{\text{ }}\]
Therefore $\cot x = \dfrac{1}{{\tan x}} = - \dfrac{5}{{12}}$
Hence, when $\sec x = \dfrac{{13}}{5}$ and x lies in fourth quadrant, the other five trigonometric ratios are :
$\cos x = \dfrac{5}{{13}}$, $\sin x = - \dfrac{{12}}{{13}}$ , $\operatorname{cosecx} = - \dfrac{{13}}{{12}}$, \[\tan x = - \dfrac{{12}}{5}\]and $\cot x = - \dfrac{5}{{12}}$
Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.\[{\sec ^2}x - {\tan ^2}x = 1\]
4.\[{\operatorname{cosec} ^2}x - {\cot ^2}x = 1\]
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:
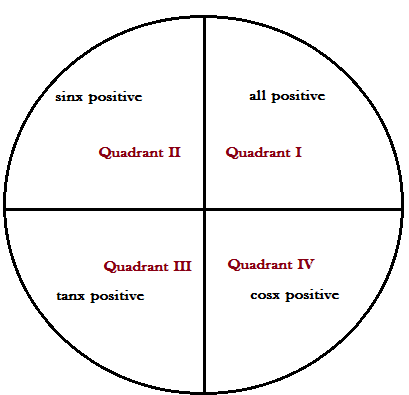
Also, note the following important formulae:
$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
${\sin ^2}x + {\cos ^2}x = 1$
\[{\sec ^2}x - {\tan ^2}x = 1\]
\[{\operatorname{cosec} ^2}x - {\cot ^2}x = 1\]
Now, the value of \[\sec x\] is given. Therefore find the value of the other five trigonometric ratios with the help of aforementioned formulae.
Complete step-by-step answer:
Given, $\sec x = \dfrac{{13}}{5}$
Therefore $\cos x = \dfrac{1}{{\sec x}} = \dfrac{5}{{13}}$
Now,
${\sin ^2}x + {\cos ^2}x = 1$
$ \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x$
Taking square root we get,
$ \Rightarrow \sin x = \pm \sqrt {1 - {{\cos }^2}x} $
On substituting the value of \[\cos x\] we get,
$ \Rightarrow \sin x = \pm \sqrt {1 - {{\left( {\dfrac{5}{{13}}} \right)}^2}} $
On simplification we get,
$ \Rightarrow \sin x = \pm \sqrt {1 - \dfrac{{25}}{{169}}} = \pm \sqrt {\dfrac{{144}}{{169}}} $
As, x lies in the fourth quadrant, so value of \[\sin x\] will be negative,
$ \Rightarrow \sin x = - \dfrac{{12}}{{13}}{\text{, }}$
Therefore, $\operatorname{cosecx} = \dfrac{1}{{\sin x}} = - \dfrac{{13}}{{12}}$
Again,
\[\because {\sec ^2}x - {\tan ^2}x = 1\]
\[ \Rightarrow {\tan ^2}x = {\sec ^2}x - 1\]
On taking square root we get,
\[ \Rightarrow \tan x = \pm \sqrt {{{\sec }^2}x - 1} \]
On substituting the value of \[\sec x\] we get,
\[ \Rightarrow \tan x = \pm \sqrt {{{\left( {\dfrac{{13}}{5}} \right)}^2} - 1} \]
On simplification we get,
\[ \Rightarrow \tan x = \pm \sqrt {\dfrac{{169}}{{25}} - 1} = \pm \sqrt {\dfrac{{144}}{{25}}} \]
As, x lies in the fourth quadrant, so value of \[\tan x\] will be negative,
\[ \Rightarrow \tan x = - \dfrac{{12}}{5}{\text{ }}\]
Therefore $\cot x = \dfrac{1}{{\tan x}} = - \dfrac{5}{{12}}$
Hence, when $\sec x = \dfrac{{13}}{5}$ and x lies in fourth quadrant, the other five trigonometric ratios are :
$\cos x = \dfrac{5}{{13}}$, $\sin x = - \dfrac{{12}}{{13}}$ , $\operatorname{cosecx} = - \dfrac{{13}}{{12}}$, \[\tan x = - \dfrac{{12}}{5}\]and $\cot x = - \dfrac{5}{{12}}$
Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.\[{\sec ^2}x - {\tan ^2}x = 1\]
4.\[{\operatorname{cosec} ^2}x - {\cot ^2}x = 1\]
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:

Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




