Question

Find the value of ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$.$$$$

Answer 1

Hint: To solve this problem, first we will use the law of exponents. Then, we will express the given number $256$ in power notation. We will use the law of exponents one more time to find required value.

Complete step-by-step solution
In this problem, to find the value of ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$, first we will use the law ${\left( {{a^m}} \right)^n} = {a^{m\; \times \;n}}$. This is called the law of exponents.
Let us compare ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$ with ${\left( {{a^m}} \right)^n}$ then we can say that $a = 256$ and $m = n = \dfrac{1}{2}$.
Now we are going to use the law ${\left( {{a^m}} \right)^n} = {a^{m\; \times \;n}}$. Therefore, ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}} = {\left( {256} \right)^{\dfrac{1}{2}\; \times \;\dfrac{1}{2}}} = {\left( {256} \right)^{\dfrac{1}{4}}}$.
Now we are going to express the number $256$ in power notation with respect to power $m \times n$. Note that here $m \times n = \dfrac{1}{4}$. Therefore, $256 = 4 \times 4 \times 4 \times 4$
$ \Rightarrow 256 = {4^4}$
$ \Rightarrow {\left( {256} \right)^{\dfrac{1}{4}}} = {\left( {{4^4}} \right)^{\dfrac{1}{4}}}$
Now again we compare ${\left( {{4^4}} \right)^{\dfrac{1}{4}}}$ with ${\left( {{a^m}} \right)^n}$ then we can say that $a = 4$ and $m = 4,n = \dfrac{1}{4}$.
Now again we will use the law ${\left( {{a^m}} \right)^n} = {a^{m\; \times \;n}}$. Therefore, ${\left( {{4^4}} \right)^{\dfrac{1}{4}}} = {\left( 4 \right)^{4\; \times \;\dfrac{1}{4}}} = {4^1} = 4$
$ \Rightarrow {\left( {256} \right)^{\dfrac{1}{4}}} = 4$
Hence, the value of ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$ is $4$.

Note: We can find the value of ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$ by another method. First we will write the prime factorization of the number $256$. Then, we will use the law of exponents.
Here $256$ is an even number. So, we can start prime factorization with number $2$.

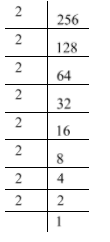
Therefore, $256 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = {2^8}$.
Now we can write ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}} = {\left[ {{{\left( {{2^8}} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$
Now we are going to use the law ${\left( {{a^m}} \right)^n} = {a^{m\; \times \;n}}$. Therefore, we can write${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}} = {\left[ {{{\left( {{2^8}} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}} = {\left( {{2^8}} \right)^{\dfrac{1}{2}\; \times \;\dfrac{1}{2}}} = {\left( {{2^8}} \right)^{\dfrac{1}{4}}}$
Now one more time we are going to use the law ${\left( {{a^m}} \right)^n} = {a^{m\; \times \;n}}$. Therefore, we can write
${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}} = {\left( {{2^8}} \right)^{\dfrac{1}{4}}} = {2^{8 \times \dfrac{1}{4}}} = {2^{\dfrac{8}{4}}} = {2^2} = 4$
Hence, the value of ${\left[ {{{\left( {256} \right)}^{\dfrac{1}{2}}}} \right]^{\dfrac{1}{2}}}$ is $4$.