Question

Find the value of following trigonometric expression:
$\dfrac{{2{\text{tan3}}{{\text{0}}^0}}}{{1{\text{ - ta}}{{\text{n}}^2}{{30}^0}}}$
A. $\cos {60^0}$
B. $s{\text{in}}{60^0}$
C. $\tan {60^0}$
D. $\sec {60^0}$

Answer 1

Hint: To solve this question we will apply the value of $\tan {30^0}$ to find the correct answer. Now we will apply the value of $\tan {30^0}$ in the given problem. So, we are going to find the value of $\tan {30^0}$. To find the value of $\tan {30^0}$ we will draw an equilateral triangle ABC of side ‘a’. We will also draw a perpendicular from AD from A to the side BC.

Complete step-by-step answer:

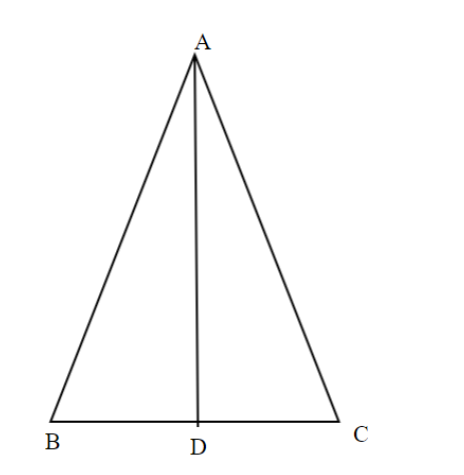
As, triangle ABC is equilateral so $\angle {\text{A = }}\angle {\text{B = }}\angle {\text{C = 6}}{{\text{0}}^0}$. Also, AD is the perpendicular. A perpendicular in an equilateral is also acts as angle – bisector and median. So, ${\text{BAD = }}\angle {\text{CAD = 3}}{{\text{0}}^0}$ and BD = DC.
Now, in $\vartriangle {\text{ABD}}$ and in $\vartriangle {\text{ACD}}$
$\angle {\text{ABD = }}\angle {\text{ACD}}$ (each equal to ${60^0}$ )
$\angle {\text{BAD = }}\angle {\text{CAD}}$ (each equal to ${30^0}$ )
BD = DC
So, $\vartriangle {\text{ABD}}$ is congruent to $\vartriangle {\text{ACD}}$ by Angle – angle – side (AAS) property.
Therefore, $\vartriangle {\text{ABD}}$
$\angle {\text{ADB = 9}}{{\text{0}}^0}$
So, applying Pythagoras theorem,
\[{\text{A}}{{\text{B}}^2}{\text{ = B}}{{\text{D}}^2}{\text{ + A}}{{\text{D}}^2}\]
\[{\text{A}}{{\text{D}}^2}{\text{ = A}}{{\text{B}}^2}{\text{ - B}}{{\text{D}}^2}\]
\[{\text{A}}{{\text{D}}^2}{\text{ = }}{{\text{a}}^2}{\text{ - }}{\dfrac{{\text{a}}}{4}^2}\]
\[{\text{AD = }}\dfrac{{\sqrt 3 a}}{2}{\text{ }}\]
$\tan {30^0}{\text{ = }}\dfrac{{{\text{BD}}}}{{{\text{AD}}}}$
$\tan {30^0}{\text{ = }}\dfrac{{\dfrac{{\text{a}}}{2}}}{{\dfrac{{\sqrt 3 a}}{2}}}{\text{ = }}\dfrac{1}{{\sqrt 3 }}$
Similarly, $\tan {60^0}{\text{ = }}\sqrt 3 $
So, applying this value in $\dfrac{{2{\text{tan3}}{{\text{0}}^0}}}{{1{\text{ - ta}}{{\text{n}}^2}{{30}^0}}}$. So
$\dfrac{{2{\text{tan3}}{{\text{0}}^0}}}{{1{\text{ - ta}}{{\text{n}}^2}{{30}^0}}}$ = $\dfrac{{2\dfrac{1}{{\sqrt 3 }}}}{{1{\text{ - (}}\dfrac{1}{{\sqrt 3 }}{)^2}^{}}}$ = $\sqrt 3 $ = $\tan {60^0}$
So, option (C) is the correct answer.

Note: Another easiest way to solve this problem is by applying the property of tan2x. In this question you have to put ${\text{x = 3}}{{\text{0}}^0}$ in the property of tan2x. By applying this method, you can get the correct answer easily. Always remember to apply the proper formula for a mistake free solution.