Question

Find the value of \[\dfrac{A\left( \Delta DEF \right)}{A\left( \Delta MNK \right)}\], given \[\Delta DEF\sim \Delta MNK\]. If DE = 2, MN = 5

Answer 1

Hint: We know that when two triangles are similar, corresponding angles and ratio of their corresponding sides are equal. So, first of all equate the corresponding angles and ratio of corresponding sides of given similar triangles and then use \[\text{Area of }\Delta \text{=}\dfrac{1}{2}ab\sin c\].

Complete step by step answer: -
Given that \[\Delta DEF\sim \Delta MNK\] and DE = 2, MN = 5.

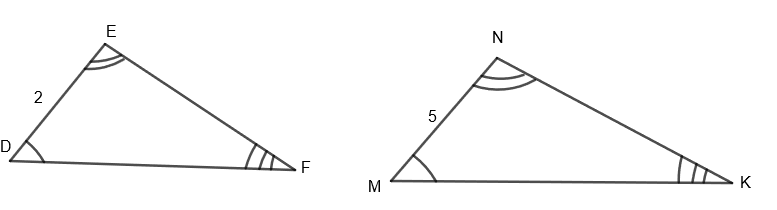
Since \[\Delta DEF\] is similar to \[\Delta MNK\], therefore the ratio of their sides would be equal. Therefore, we get,
\[\dfrac{DE}{MN}=\dfrac{EF}{NK}=\dfrac{FD}{KM}\]
Substituting DE = 2 and MN = 5. We get,
\[\dfrac{DE}{MN}=\dfrac{EF}{NK}=\dfrac{FD}{KM}=\dfrac{2}{5}....\left( i \right)\]
Also, in similar triangles, corresponding angles are equal. Here we get
\[\angle D=\angle M\]
\[\angle E=\angle N\]
\[\angle F=\angle K\]
Now, we know that \[\text{Area of }\Delta \text{=}\dfrac{1}{2}ab\sin c\] where a and b are any two sides of triangle and c is the angle between them.Therefore,
\[\dfrac{\text{Area}\left( \Delta DEF \right)}{\text{Area}\left( \Delta MNK \right)}=\dfrac{\dfrac{1}{2}DE.FD.\sin D}{\dfrac{1}{2}MN.KM.\sin M}\]
As \[\angle D=\angle M,\text{ }\sin D=\sin M\]
\[\dfrac{\text{Area}\left( \Delta DEF \right)}{\text{Area}\left( \Delta MNK \right)}=\left( \dfrac{DE}{MN} \right).\left( \dfrac{FD}{KM} \right)\]
By equation (i),
\[\dfrac{DE}{MN}=\dfrac{FD}{KM}=\dfrac{2}{5}\]
Hence,
\[\dfrac{\text{Area}\left( \Delta DEF \right)}{\text{Area}\left( \Delta MNK \right)}=\left( \dfrac{2}{5} \right).\left( \dfrac{2}{5} \right)={{\left( \dfrac{2}{5} \right)}^{2}}=\dfrac{4}{25}\]

Note: Here students must take care of equating the “corresponding” parts of given triangles. Like here DE must be taken in similarity with MN and not with any other side as given in question. Similar rules must be followed for other sides and angles.