Question

Find the value of D. \[\]

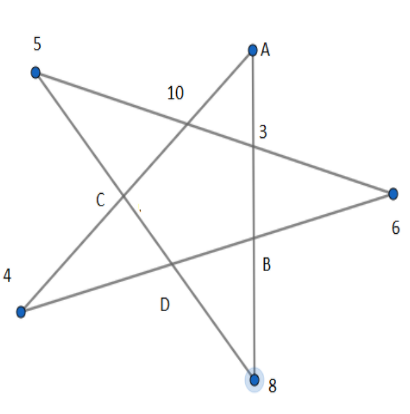
Answer 1

Hint: We observe the side 5, 10, 3, 6. We see that the sum of all the values on that side is 24. We use the fact that in a magic pentagram the sum of values on all sides or a line is equal. We take different sides, which have unknown A and C form linear equations. We assume different values A starting with A=1 and check if the obtained value of D satisfies the side with 4, D, B, 3.\[\]

Complete step-by-step solution

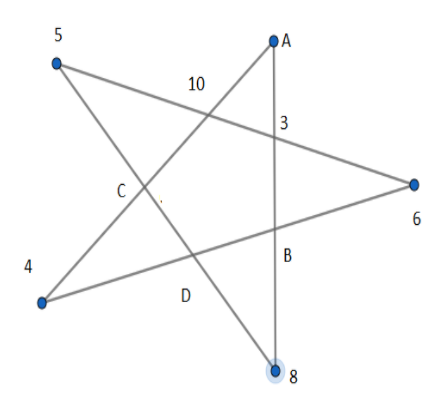
We see that the given figure is a five-pointed star whose vertices and points of intersection of sides are represented by a given and unknown numerical value. One such unknown is D whose value we are asked to determine.
We can guess the different rules for vertices, edges and points of intersection. \[\]
We know that in such problems involving magical pentagram we have to use addition operation on all the positive integral values on sides and sum on all sides will be equal. Let us see the side with values 5, 10, 3, 6. The sum of all values on that edge is
\[5+10+3+6=24\]
We similarly take the side with values A, 3, B,8. As sum on all the sides are equal we have
\[\begin{align}
  & A+3+8+B=24 \\
 & \Rightarrow A+B=24-11=13....(1) \\
\end{align}\]
We take the side with values A, 10, C, 4 and get,
\[\begin{align}
  & A+10+C+4=24 \\
 & \Rightarrow A+C=24-14=10....(2) \\
\end{align}\]
We take the side with values 5, C, D, 8 and get,
\[\begin{align}
  & 5+C+D+8=24 \\
 & \Rightarrow C+D=24-13=11....(3) \\
\end{align}\]
Let us check 4, D, B, 6 and get ,
\[\begin{align}
  & 4+D+B+6=24 \\
 & \Rightarrow D+B=14...\left( 4 \right) \\
\end{align}\]
Let assume $A=1$ and we obtain from equation (1), (2) , (3)
\[B=12,C=9,D=2\]
We put the value in (4) and check the satisfaction as
\[B+D=12+2=14\]
So we have one value for D is 2. Let us assume $A=2$ we obtain from equation (1), (2), (3),
\[B=11,C=8,D=3\]
We put the value in (4) and check the satisfaction as
 \[B+D=11+3=14\]
Similarly we can take $A=3,4,...,9$ since $C+D=10$ and find the corresponding value of D. The possible values of D are
\[D=2,3,4,5.6,7,8,9,10\]
All of these values of D are going to satisfy the line 4, D, B, 6 because we are going to get 9 solutions for the quadruple $\left( A,B,C,D \right)$ which are
\[\begin{align}
  & \left( 1,12,9,2 \right),\left( 2,11,8,3 \right),\left( 3,10,7,4 \right),\left( 4,9,6,5 \right),\left( 5,8,5,6 \right),\left( 6,7,4,7 \right) \\
 & \left( 7,6,3,8 \right),\left( 8,5,2,9 \right),\left( 9,4,1,10 \right) \\
\end{align}\]

Note: The problems of such type are called magic pentagram puzzles. If all the values on the vertices and points of intersection are primes then it is called a prime magical pentagram puzzle. Another such puzzle with additions is a magical square where the sum of rows and columns are equal.