Question

How do you find the value of $ \cot \left( {{{180}^\circ }} \right) $ ?

Answer 1

Hint: In the given problem, we are required to find the cotangent of a given angle using some simple and basic knowledge about the concepts of trigonometry and its properties. Such questions essentially require prerequisite knowledge of the unit circle and its applications in these types of questions. Unit circle is a circle with a radius of one unit drawn on a graph paper with its centre at origin.

Complete step by step solution:
Consider a unit circle (a circle of radius of 1 unit centered at origin). We need to find out the value of $ \cot \left( {{{180}^\circ }} \right) $ using the unit circle.
So, we have, $ \cot \left( {{{180}^\circ }} \right) $ .
The conversion of an angle from degrees to radians is simple. One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. A simple and direct conversion from degree measure to radian measure is $ {180^ \circ } = \pi \,Radians $ .
So, converting degrees into radians, we get,
 $ \cot \left( {{{180}^\circ }} \right) $ $ = \cot \left( \pi \right) $
Since cotangent and tangent functions are periodic functions with fundamental period of $ \pi $ , so the value of cotangent and tangent function gets repeated after intervals in multiples of $ \pi $ . Hence, we can say that the value of $ \cot \left( \pi \right) $ is same as $ \cot \left( 0 \right) $ .

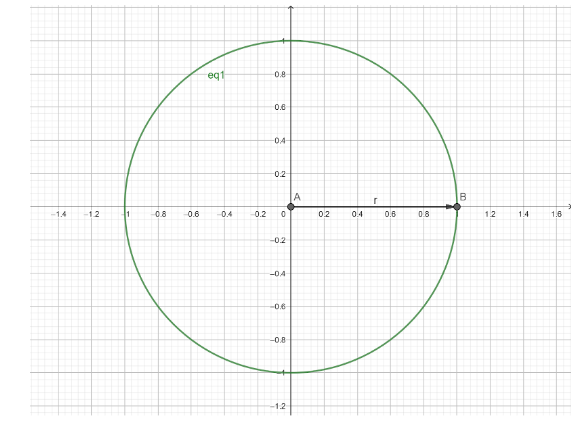
Now, when we observe the unit circle, we notice that a line is formed instead of a right angled triangle due to which the perpendicular or the altitude of the supposed right angled triangle tends to zero.
We also know that $ \cot \theta = \left( {\dfrac{{Base}}{{Perpendicular}}} \right) $ .
So, the denominator for the expression of $ \cot \left( 0 \right) $ tends to zero. So, the value of $ \cot \left( 0 \right) $ is undefined.
Similarly, due to periodicity of the cotangent function, the value of $ \cot \left( {{{180}^ \circ }} \right) $ is undefined.
So, the correct answer is “ Undefined.”.

Note: Periodic Function is a function that repeats its value after a certain interval. For a real number $ T > 0 $ , $ f\left( {x + T} \right) = f\left( x \right) $ for all x. If T is the smallest positive real number such that $ f\left( {x + T} \right) = f\left( x \right) $ for all x, then T is called the fundamental period. The value of $ \cot \left( {{{180}^ \circ }} \right) $ could also be computed using the graph of cotangent function.