Question

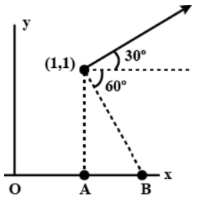
Find the torque about point O and A. \[\hat F = 5\sqrt 3 \hat i + 5\hat j\]

     

Answer 1

Hint:You can solve the question by simply recalling that torque is nothing but the cross-product of position vector with the force vector. It is shown in the diagram that the force is acting at $\left( {1,1} \right)$. To find the torque at point O, find the cross-product of its relative position vector with the given force vector in the question, proceed similarly for the point A.

Complete step by step answer:
We will be proceeding with the solution exactly as described in the hint section of the solution to the question.
To find the torque about point O, we first need to define its relative position vector. We have already been given the coordinates of the point where the force is acting. To find the torque about O, we can write:
$
  {\overrightarrow O _{rel}} = (\hat i + \hat j) - \left( {0\hat i + 0\hat j} \right) \\
  {\overrightarrow O _{rel}} = \hat i + \hat j \\
 $
Now, all we need to do is to find the cross-product of the relative position vector and the force vector as:
$\overrightarrow {{\tau _o}} = {\overrightarrow O _{rel}} \times \overrightarrow F $
We have already found out the value of the relative position vector, the force vector is given in the question.
Substituting the values, we get:
$\overrightarrow {{\tau _o}} = \left( {\hat i + \hat j} \right) \times \left( {5\sqrt 3 \hat i + 5\hat j} \right)$
Now, we already know cross-products of the coordinate vectors as:
\[
  \hat i \times \hat i = \hat j \times \hat j = 0 \\
  \hat i \times \hat j = \hat k \\
  \hat j \times \hat i = - \hat k \\
 \]
Using these results here, we get:
$\overrightarrow {{\tau _o}} = 5\hat k - 5\sqrt 3 \hat k = 5\left( {1 - \sqrt 3 } \right)\,\hat k$
Similarly, for point A, the coordinates of the point are $\left( {1,0} \right)$. Using this, we can find its relative position vector as:
$
  {\overrightarrow A _{rel}} = \left( {\hat i + \hat j} \right) - \left( {\hat i} \right) \\
  {\overrightarrow A _{rel}} = \hat j \\
 $
Now the we’ve found out the relative position vector for point A, we can use it to find the torque about point A as:
$\overrightarrow {{\tau _A}} = \left( {{{\overrightarrow A }_{rel}}} \right) \times \overrightarrow F $
Now, substituting in the values, we get:
$
  \overrightarrow {{\tau _A}} = \left( {\hat j} \right) \times \left( {5\sqrt 3 \hat i + 5\hat j} \right) \\
  \overrightarrow {{\tau _A}} = - 5\sqrt 3 \,\hat k \\
 $
Here, we have found the answer to both the parts of the question as:
$\overrightarrow {{\tau _o}} = 5\left( {1 - \sqrt 3 } \right)\,\hat k$
$\overrightarrow {{\tau _A}} = - 5\sqrt 3 \,\hat k$

Note:Many students make mistakes in the cross-products of the coordinate vectors and thus get opposite signs of their cross-products. If only the magnitude and angle of force would have been given, you could use the other formula of cross-product as:
$\overrightarrow \tau = Fr\sin \theta \,\hat n$