Question

How do you find the Taylor polynomial of degree $n = 4$ for $x$ near the point $a = \pi $ for the function $\cos x$?

Answer 1

Hint: We need to calculate the derivatives of the above function at $x = \pi $. Calculate $f'\left( x \right)$, $f''\left( x \right)$, $f'''\left( x \right)$, ${f^{\left( 4 \right)}}\left( x \right)$ at $x = \pi $. Next, put $n = 4$ and $a = \pi $in the Taylor polynomial of degree $n$. Then, put the value of $f\left( \pi \right)$, $f'\left( \pi \right),f''\left( \pi \right),f'''\left( \pi \right),{f^{\left( 4 \right)}}\left( \pi \right)$.

Formula used:
The Taylor polynomial of degree $n$. Approximating $f\left( x \right)$ for $x$ near $a$ is given by
$f\left( x \right) \approx {P_n}\left( x \right) = f\left( a \right) + f'\left( a \right)\left( {x - a} \right) + \dfrac{{f''\left( a \right)}}{{2!}}{\left( {x - a} \right)^2} + ... + \dfrac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x - a} \right)^n}$
We call ${P_n}\left( x \right)$ the Taylor polynomial of degree $n$ centered at $x = a$ or the Taylor polynomial about $x = a$.

Complete step by step answer:
Function $f\left( x \right)$ is given as
$f\left( x \right) = \cos x$
And
$n = 4$
$a = \pi $
Now we need to calculate the derivatives of the above function at $x = \pi $.
So, first differentiate $f$ with respect to $x$.
$f'\left( x \right) = \dfrac{d}{{dx}}\left( {\cos x} \right)$
Now, use property that differentiation of $\cos x$ with respect to $x$ is $ - \sin x$,
i.e., $\dfrac{d}{{dx}}\left( {\cos x} \right) = - \sin x$.
So, $f'\left( x \right) = - \sin x$
Now, calculate $f'\left( x \right)$ at $x = \pi $.
$f'\left( \pi \right) = - \sin \pi $
Since the exact value of $\sin \pi $ is $0$, i.e., $\sin \pi = 0$.
Thus, $f'\left( \pi \right) = 0$…(i)
Now, differentiate $f'$ with respect to $x$.
$f''\left( x \right) = - \dfrac{d}{{dx}}\left( {\sin x} \right)$
Now, use property that differentiation of $\sin x$ with respect to $x$ is $\cos x$,
i.e., $\dfrac{d}{{dx}}\left( {\sin x} \right) = \cos x$.
So, $f''\left( x \right) = - \cos x$
Now, calculate $f''\left( x \right)$ at $x = \pi $.
$f''\left( \pi \right) = - \cos \pi $
Since the exact value of $\cos \pi $ is $ - 1$, i.e., $\cos \pi = - 1$.
Thus, $f''\left( \pi \right) = 1$…(ii)
Now, differentiate \[f''\] with respect to $x$.
$f'''\left( x \right) = - \dfrac{d}{{dx}}\left( {\cos x} \right)$
Now, use property that differentiation of $\cos x$ with respect to $x$ is $ - \sin x$,
i.e., $\dfrac{d}{{dx}}\left( {\cos x} \right) = - \sin x$.
So, $f'''\left( x \right) = \sin x$
Now, calculate $f'''\left( x \right)$ at $x = \pi $.
$f'''\left( \pi \right) = \sin \pi $
Since the exact value of $\sin \pi $ is $0$, i.e., $\sin \pi = 0$.
Thus, $f'''\left( \pi \right) = 0$…(iii)
Now, differentiate ${f^{\left( 3 \right)}}$ with respect to $x$.
${f^{\left( 4 \right)}}\left( x \right) = \dfrac{d}{{dx}}\left( {\sin x} \right)$
Now, use property that differentiation of $\sin x$ with respect to $x$ is $\cos x$,
i.e., $\dfrac{d}{{dx}}\left( {\sin x} \right) = \cos x$.
So, ${f^{\left( 4 \right)}}\left( x \right) = \cos x$
Now, calculate ${f^{\left( 4 \right)}}\left( x \right)$ at $x = \pi $.
${f^{\left( 4 \right)}}\left( \pi \right) = \cos \pi $
Since the exact value of $\cos \pi $ is $ - 1$, i.e., $\cos \pi = - 1$.
Thus, ${f^{\left( 4 \right)}}\left( \pi \right) = - 1$…(iv)
Since, the Taylor polynomial of degree $n$. Approximating $f\left( x \right)$ for $x$ near $a$ is given by
$f\left( x \right) \approx {P_n}\left( x \right) = f\left( a \right) + f'\left( a \right)\left( {x - a} \right) + \dfrac{{f''\left( a \right)}}{{2!}}{\left( {x - a} \right)^2} + ... + \dfrac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x - a} \right)^n}$…(v)
We call ${P_n}\left( x \right)$ the Taylor polynomial of degree $n$ centered at $x = a$ or the Taylor polynomial about $x = a$.
Put $n = 4$ in equation (v).
$f\left( x \right) \approx {P_4}\left( x \right) = f\left( a \right) + f'\left( a \right)\left( {x - a} \right) + \dfrac{{f''\left( a \right)}}{{2!}}{\left( {x - a} \right)^2} + \dfrac{{f'''\left( a \right)}}{{3!}}{\left( {x - a} \right)^3} + \dfrac{{{f^{\left( 4 \right)}}\left( a \right)}}{{4!}}{\left( {x - a} \right)^4}$
Now, put $a = \pi $ in above equation.
$ \Rightarrow f\left( x \right) \approx {P_4}\left( x \right) = f\left( \pi \right) + f'\left( \pi \right)\left( {x - \pi } \right) + \dfrac{{f''\left( \pi \right)}}{{2!}}{\left( {x - \pi } \right)^2} + \dfrac{{f'''\left( \pi \right)}}{{3!}}{\left( {x - \pi } \right)^3} + \dfrac{{{f^{\left( 4 \right)}}\left( \pi \right)}}{{4!}}{\left( {x - \pi } \right)^4}$
Put the value of $f'\left( \pi \right),f''\left( \pi \right),f'''\left( \pi \right),{f^{\left( 4 \right)}}\left( \pi \right)$ from equation (i), (ii), (iii) and (iv) respectively.
$ \Rightarrow f\left( x \right) \approx {P_4}\left( x \right) = f\left( \pi \right) + \left( 0 \right)\left( {x - \pi } \right) + \dfrac{1}{{2!}}{\left( {x - \pi } \right)^2} + \dfrac{0}{{3!}}{\left( {x - \pi } \right)^3} + \dfrac{{\left( { - 1} \right)}}{{4!}}{\left( {x - \pi } \right)^4}$
Now, calculate $f\left( \pi \right)$ using $\cos \pi = - 1$.
Since, $f\left( x \right) = \cos x$
Thus, $f\left( \pi \right) = - 1$.
$ \Rightarrow f\left( x \right) \approx {P_4}\left( x \right) = - 1 + \dfrac{1}{{2!}}{\left( {x - \pi } \right)^2} - \dfrac{1}{{4!}}{\left( {x - \pi } \right)^4}$
It can be written as
$ \Rightarrow f\left( x \right) \approx {P_4}\left( x \right) = - 1 + \dfrac{{{{\left( {x - \pi } \right)}^2}}}{2} - \dfrac{{{{\left( {x - \pi } \right)}^4}}}{{24}}$

Therefore, the Taylor polynomial of degree $n = 4$ for $x$ near the point $a = \pi $ for the function $\cos x$ is $ - 1 + \dfrac{{{{\left( {x - \pi } \right)}^2}}}{2} - \dfrac{{{{\left( {x - \pi } \right)}^4}}}{{24}}$.

Note: We can check $ - 1 + \dfrac{{{{\left( {x - \pi } \right)}^2}}}{2} - \dfrac{{{{\left( {x - \pi } \right)}^4}}}{{24}}$ is the Taylor polynomial of degree $n = 4$ for $x$ near the point $a = \pi $ for the function $\cos x$ by plotting these on graph paper.

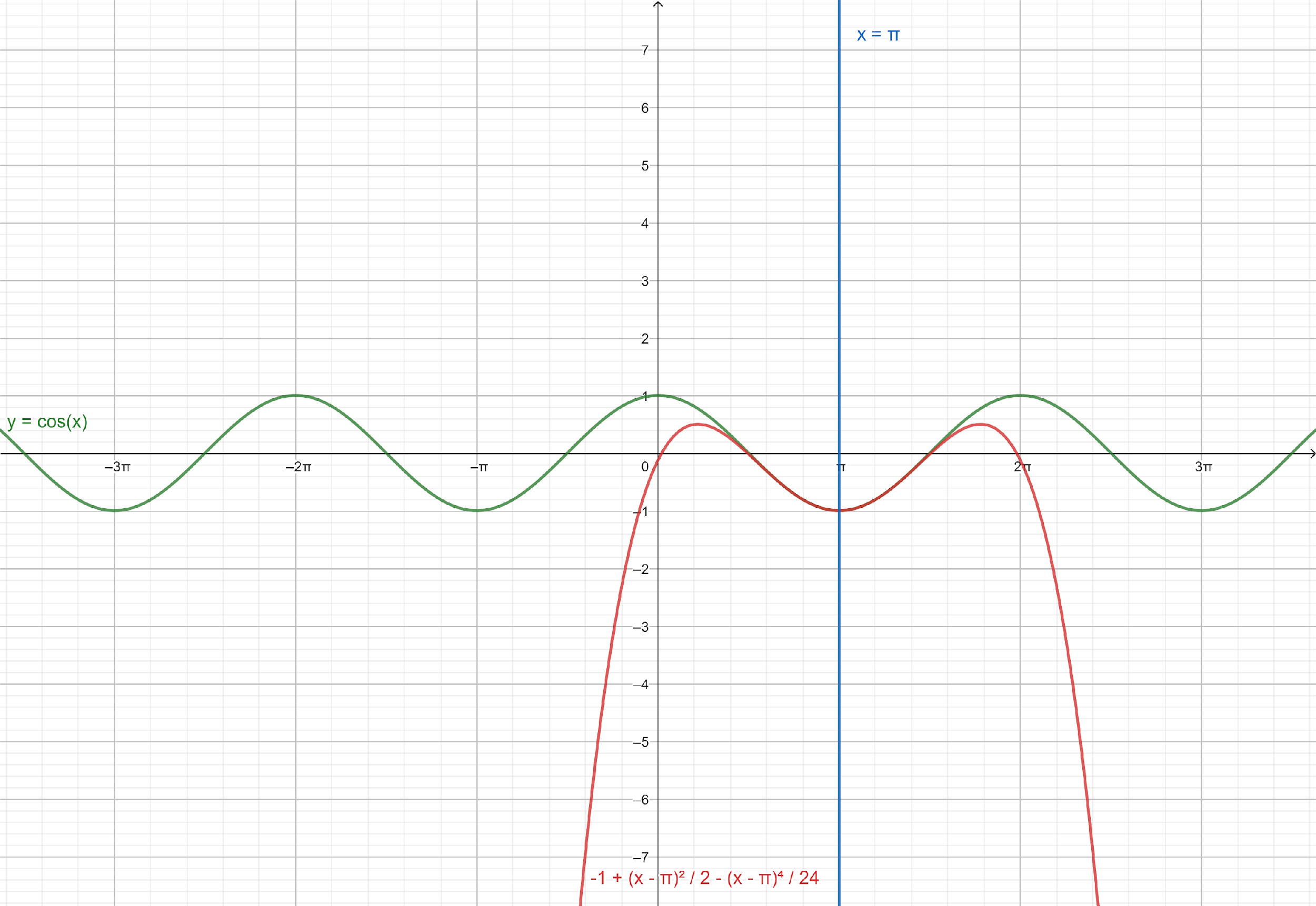
Final solution: Therefore, the Taylor polynomial of degree $n = 4$ for $x$ near the point $a = \pi $ for the function $\cos x$ is $ - 1 + \dfrac{{{{\left( {x - \pi } \right)}^2}}}{2} - \dfrac{{{{\left( {x - \pi } \right)}^4}}}{{24}}$.