Question

Find the summation of two vectors where the angle between the two vectors is $ \theta $ .

Answer 1

Hint : The angle between two vectors is considered the angle subtended from one to the other when the vectors are placed tail to tail. When the vectors are placed head to tail, the sum of the vector is another vector running from the tail of one to the head of the other.

Formula used: In this solution we will be using the following formula;
cosine rule: $ \left| {\vec A + \vec B} \right| = \sqrt {{A^2} + {B^2} - 2AB\cos \left( {180 - \theta } \right)} $ where $ \left| {\vec A + \vec B} \right| $ is the magnitude of the sum of any vector, $ A $ and $ B $ are the individual vectors placed head to tail, and $ \theta $ is the acute angle between them. $ \beta = {\tan ^{ - 1}}\left( {\dfrac{{B\sin \theta }}{{A + B\cos \theta }}} \right) $ where $ \beta $ is the direction of the sum of any two vectors , $ A $ and $ B $ .

Complete step by step answer

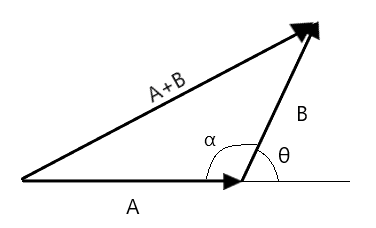
Geometrically, the sum of a vector is given as shown above. When adding two vectors, the vectors are placed head to tail, then the sum is the vector drawn from the tail of the first vector to the head of the other. However, it can be proven that $ \vec A + \vec B = \vec B + \vec A $ . The angle theta $ \theta $ between them is considered the acute angle subtended if one is to orient one in the same direction as another, if the vectors are placed tail to tail. In the figure above, if we are to displace the $ \vec B $ to the left without changing the orientation until the tail coincides with the tail of $ \vec A $ , then the angle subtended by $ \vec A $ if it is to orient itself to face the direction of $ \vec B $ is considered the angle between two vectors. We must note that it’ll be equal to $ \theta $ from the diagram.
Now, algebraically, from the cosine rule, the line $ \left| {\vec A + \vec B} \right| $ is given as
 $\Rightarrow \left| {\vec A + \vec B} \right| = \sqrt {{A^2} + {B^2} - 2AB\cos \alpha } $
But $ \alpha = 180 - \theta $ , then
 $\Rightarrow \left| {\vec A + \vec B} \right| = \sqrt {{A^2} + {B^2} - 2AB\cos \left( {180 - \theta } \right)} $
Also, $ \cos \left( {180 - \theta } \right) = - \cos \theta $
Hence, by substitution
 $\Rightarrow \left| {\vec A + \vec B} \right| = \sqrt {{A^2} + {B^2} + 2AB\cos \theta } $
And this is the magnitude of the sum.
From trigonometry, the direction is given as
 $\Rightarrow \beta = {\tan ^{ - 1}}\left( {\dfrac{{B\sin \theta }}{{A + B\cos \theta }}} \right) $ .

Note
To avoid confusions, let us proof that $ \cos \left( {180^\circ - \theta } \right) = - \cos \theta $ From a trigonometric identity,
 $\Rightarrow \cos \left( {180 - \theta } \right) = \sin 180^\circ \sin \theta + \cos \theta \cos 180^\circ $ ,
Since, $ \sin 180^\circ = 0 $ and $ \cos 180^\circ = - 1 $
Hence, by substitution, we have that
 $\Rightarrow \sin 180^\circ \sin \theta + \cos \theta \cos 180^\circ = 0 + \left( { - 1\cos \theta } \right) = - \cos \theta $
Hence,
 $\Rightarrow \cos \left( {180 - \theta } \right) = - \cos \theta $ .