Question

How do you find the solution set for \[y=6x-5\] and \[y=-x+9\]?

Answer 1

Hint: In order to find the solution of the given question that is to find the solution set for the system of equations \[y=6x-5\] and \[y=-x+9\], use the substitution method. This method works by solving one of the linear equations for one of the variables, then substituting this value for the same variable in the other linear equation and solving for the other variable. It does not matter which equation you choose first, or which variable you solve for first; the values for both variables will be the same.

Complete step-by-step solution:
According to the question, given system of equation is as follows:
\[\begin{align}
  & y=6x-5 \\
 & y=-x+9 \\
\end{align}\]
The first step would be to choose one of the equations and solve it for either \[x\] or \[y\]to apply the substitution method. As you can see that \[y\] is equal to two distinct expressions that depend on \[x\], which can only mean that these expressions must be equal to each other.
Therefore, we can write:
\[\Rightarrow 6x-5=-x+9\]
Now solve this equation to find the value of \[x\], take the terms with variable \[x\] on the left-hand-side and the constant terms to the right-hand-side, we get:
\[\Rightarrow 6x+x=9+5\]
After simplifying the terms on both the sides we get:
\[\Rightarrow 7x=14\]
Now simplify it further by dividing the coefficient of \[x\] to the right-hand-side, we get:
\[\Rightarrow x=\dfrac{14}{7}\]
Finally, after solving the division we get:
\[\Rightarrow x=2\]
To find the value of \[y\], substitute the value of \[x\] to any one of the original equations.
Let us substitute the value of \[x\] in the equation \[y=6x-5\] we get:
\[\Rightarrow y=6\cdot \left( 2 \right)-5\]
After solving the brackets, we get:
\[\Rightarrow y=12-5=7\]
\[\Rightarrow y=7\]
Therefore, the solution set to this system of equations \[y=6x-5\]and \[y=-x+9\] is
\[\left\{ \begin{align}
  & x=2 \\
 & y=7 \\
\end{align} \right\}\]

Note: There's an alternative method to solve the given question that is by plotting the graph.
A linear equation can be represented by a line in the \[x,y\]-plane. The solution to a system of linear equations is the point at which the lines representing the linear equations intersect.
Plotting the given system of equation in the following graph:

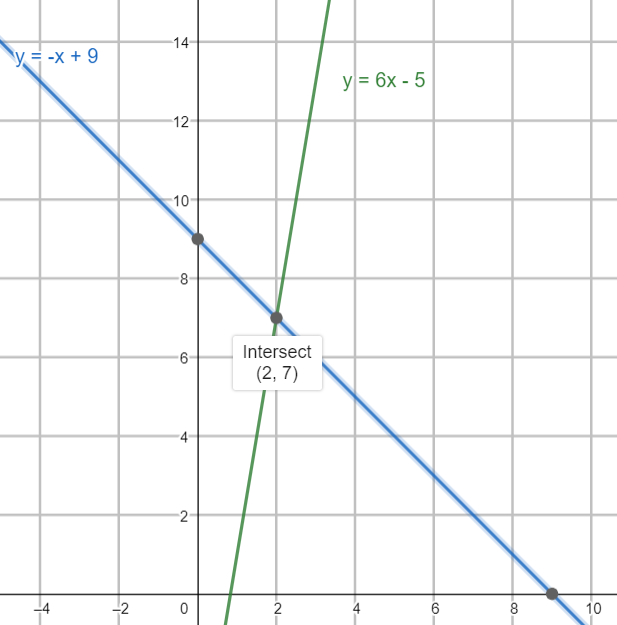
Here the two lines have two different slopes and they have one intersection point.
Therefore, the system of equations has exactly one solution that is \[\left\{ \begin{align}
  & x=2 \\
 & y=7 \\
\end{align} \right\}\]