Question

How do you find the slope of the line $x = - 6$ ?

Answer 1

Hint: In this question, we are given an equation of a line and we have been asked to find its slope. There are 2 ways to solve this question.
Method 1: Find the type of line the equation is making by plotting it on the graph. Then, find the slope of the equation.
Method 2: This method involves the use of the concept of parallel lines and perpendicular lines. Find out the axis to which the given line is parallel or perpendicular and then, use their concept to find the slope of the line.

Formula used: Slope = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$

Complete step-by-step solution:
We are given an equation $x = - 6$. Let us plot this on the graph. It will look like:

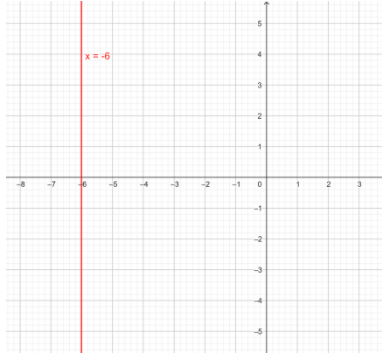
Let us assume any two points that lie on this line. They will be $\left( { - 6,a} \right)$ and $\left( { - 6,b} \right)$.
Let us put these two points in the formula of slope, Slope = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$,
Slope = $\dfrac{{b - a}}{{ - 6 - \left( { - 6} \right)}}$
Simplifying it would give us –
Slope = $\dfrac{{b - a}}{0}$

Therefore, the slope of the given line is undefined. It also shows that the slope of a vertical line is undefined.

Note: We have read that the slope of x-axis is equal to $0$ and slope of y-axis is equal to undefined.
As we can see in the above graph, the given line is parallel to the y-axis. We read that slope of parallel lines are equal, i.e., ${m_1} = {m_2}$ and the product of the slope of perpendicular lines is equal to $ - 1$, i.e., ${m_1}.{m_2} = - 1$.
Now, using this concept of slopes and parallel lines, we can say that since the given line is parallel to the y-axis and the slope of the y-axis is undefined, the slope of the given line is also undefined.