Question

How do you find the slope and ‘y’ intercept of $ x+4y=12 $?

Answer 1

Hint: We are asked to find the slope and the ‘y’ intercept, do the same we will learn about the slope of a line, y-intercept, x-intercept, we will use that the slope-intercept form of the line is given as $ y=mx+c $ where ‘m’ is the slope of the line which ‘c’ is the y-intercept, we change one given problem and then compare 1st with $ y=mx+c $ slope-intercept term to find the value of slope ‘m’.

Complete step by step answer:
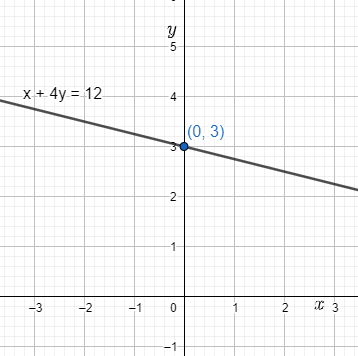
We are given $ x+4y=12 $
We are asked to find the slope and the y-intercept.
Before we move forward, we will learn what does the slope of a line and y-intercept or x-intercept mean.
The X-intercept of a line denotes the coordinate of the line at which the line will cut past the x-axis.
At this point since it touches the x-axis.
So, at x-intercept ‘y’ is always zero to find the x-intercept we will put y=0 in the given equation and solve for the value of x.
As we have our equation as $ x+4y=12 $ putting y=0, we get –
 $ \begin{align}
  & x+4\times 0=12 \\
 & x+0=12 \\
 & x=12 \\
\end{align} $
So, x-intercept is 12.
Now, the y-intercept of a line denotes those coordinates of the line at which it will cut the y-axis.
At this point since it touches the y-axis so the coordinate of the x-axis is always zero.
So, to find the y-intercept, we usually put x=0 and solve for the value of ‘y’.
As we have our equation as –
 $ x+4y=12 $
So, we put x=0, we get –
 $ \begin{align}
  & 0+4y=12 \\
 & 4y=12 \\
\end{align} $
Dividing both side by ‘4’, we get –
 $ \dfrac{4y}{4}=\dfrac{12}{4} $
By simplifying, we get –
 $ y=3 $
So we get the line $ x+4y=12 $ cut the y-axis at $ \left( 0,3 \right) $ y-intercept is $ y=3 $ .
Now, the slope of a line is usually defined as the angle made by the line with the positive x-axis, mathematically using coordinate geometry we find the slope by finding the rate of change of y-coordinate with respect to the x-coordinates
We also know that for any standard equation line.
 $ ax+by+c=0 $ , we can transform this equation into slope intercept term.
Slope intercept term of the line is given as –
 $ y=mx+c $
Where ‘m’ is the slope.
Now, we have $ x+4y=12 $ , we want to find the slope so we change the equation into the slope-intercept term.
So, we subtract ‘x’ from both side of $ x+4y=12 $
We get –
 $ x+4y-x=-x+12 $
As $ x-x=0 $ so, we get –
 $ 4y=-x+12 $
Dividing both side by ‘4’, we have –
 $ y=\dfrac{-x}{4}+\dfrac{12}{4} $
 $ y=\dfrac{-1}{4}x+3 $
So, we compare this with slope-intercept term $ y=mx+c $
We get –
 $ m=\dfrac{-1}{4} $ , so the slope of the line is $ \dfrac{-1}{4} $ .

Note:
Remember that we cannot add the variable to the constant. Usually, mistakes like this which one adds constantly with variables usually happen.
For example, $ 3x+6=9x $, here one added 6 with 3 of x made it 9x.
This is wrong, we cannot add constants and variables at once. Only the same variables are added to each other.