Question

How do you find the slope and intercept to graph $2x-6y=12$ ?

Answer 1

Hint: We should know about the different general equation of a line. There are several ways in which we can express a line. There is slope form, slope intercept form, normal form. But here, let us talk about the slope intercept form. The general equation of slope intercept form of a line is $y=mx+c$ where $m$ is the slope of the line and $c$ is a constant which gives us the length of the intercept that line cut off on the $y$-axis.

Complete step by step solution:
The line given to us is $2x-6y=12$.
We can see that the entire line equation is divisible by $2$.
So let us divide the entire equation by $2$.
Upon doing so, we get the following :
$\begin{align}
  & \Rightarrow 2x-6y=12 \\
 & \Rightarrow x-3y=6 \\
\end{align}$
The line equation that we find the slope and intercept of is $x-3y=6$.
 Let us send the $y$term onto the right hand side of the equation from the left hand side.
Upon doing so, we get the following :
$\begin{align}
  & \Rightarrow x-3y=6 \\
 & \Rightarrow x=6+3y \\
\end{align}$
Now let us send the constant $6$onto the left hand side from the right hand side.
Upon doing so, we get the following :
$\begin{align}
  & \Rightarrow x-3y=6 \\
 & \Rightarrow x=6+3y \\
 & \Rightarrow x-6=3y \\
\end{align}$
Now let us divide the entire expression with $3$.
Upon doing so, we get the following :
$\begin{align}
  & \Rightarrow x-3y=6 \\
 & \Rightarrow x=6+3y \\
 & \Rightarrow x-6=3y \\
 & \Rightarrow \dfrac{x}{3}-2=y \\
 & \Rightarrow y=\dfrac{x}{3}-2 \\
\end{align}$
Let us compare$y=\dfrac{x}{3}-2$ with the general form of slope intercept form $y=mx+c$.
We can clearly see that the coefficient of the $x$ represents the slope. So the slope,$m$, of the given line is $\dfrac{1}{3}$. The constant,$c$, of the given line is $-2$.
The line has cut off an intercept on the negative $y$-axis since the constant is negative.
Graph :

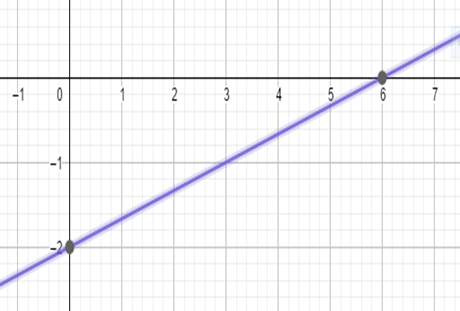
Note: We have to remember all the general equations of all forms of lines so as to complete the question quickly. We should be careful while comparing the given line equation with the general form or else the graph or the entire answer will go wrong.