Question

Find the slant height of the cone, whose volume is 1232\[c{m^3}\] and height is 24cm.

Answer 1

Hint- Equate the Volume formula to the Volume that is given and find out R. Then substitute the value of R and H in the Slant height formula(L).

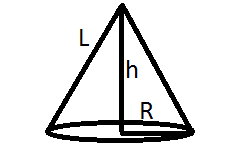
i.e. \[Volume = \dfrac{1}{3}\pi {R^2}h\] and \[{L^2} = {R^2} + {h^2}\]

Complete step-by-step answer:

Here volume V=1232\[c{m^3}\] and height h=24cm
Using formula of volume we get, V=\[Volume = \dfrac{1}{3}\pi {R^2}h\]
Then equating the given volume with the formula of volume we get,
\[1232 = \dfrac{1}{3}\pi {R^2}(24)\]
Then putting the value of $\pi = \dfrac{{22}}{7}$ we get,
\[
  1232 = \dfrac{1}{3} \times \dfrac{{22}}{7}{R^2}(24) \\
  1232 \times 3 \times \dfrac{7}{{22}} \times \dfrac{1}{{24}} = {R^2} \\
  R = \sqrt {49} \\
  R = 7cm \\
\]
Since the square root of 49 is 7.
And now, we need to find the slant height of the cone L.
As we know ${L^2} = {R^2} + {H^2}$
Putting the value of R and H we get,
\[
  {L^2} = {(7)^2} + {(24)^2} \\
  {L^2} = 49 + 576 \\
  L = \sqrt {625} \\
  L = 25cm \\
\]
Since the square root of 625 is 25.

Hence the answer to this question is 25cm.

Note- For solving such problems we need to memorize the basic formulae and fundamentals of the chapter of volume of solid figures. We basically commit mistakes in identifying what needs to be calculated and Incorrect use of Formulae.