Question

Find the shifted equation of $ {{x}^{2}}+{{y}^{2}}=49 $ when the graph is shifted 3 units down and 2 units left.

Answer 1

Hint: We first try to understand the impact for shifting the graph. We use two coordinates as of a point’s previous and after value. We find the relation between those two coordinates. We replace the values according to the relation and find the shifted equation.

Complete step by step answer:
We need to find the shifted equation of $ {{x}^{2}}+{{y}^{2}}=49 $ when the graph is shifted 3 units down and 2 units left.
For shifting the graph, the respective position of a point has changed according to the shift of the graph.
The graph is shifted 3 units down and 2 units left. The effects are changes in x (for left-right movement) and y (for up-down movement) coordinates. A graph has gone down which in turn has increased the y coordinates of a fixed point and it has gone left which in turn has increased the x coordinates. The origin of the previous graph $ O\left( 0,0 \right) $ changes to $ A\left( -2,-3 \right) $ , new origin of the shifted graph.

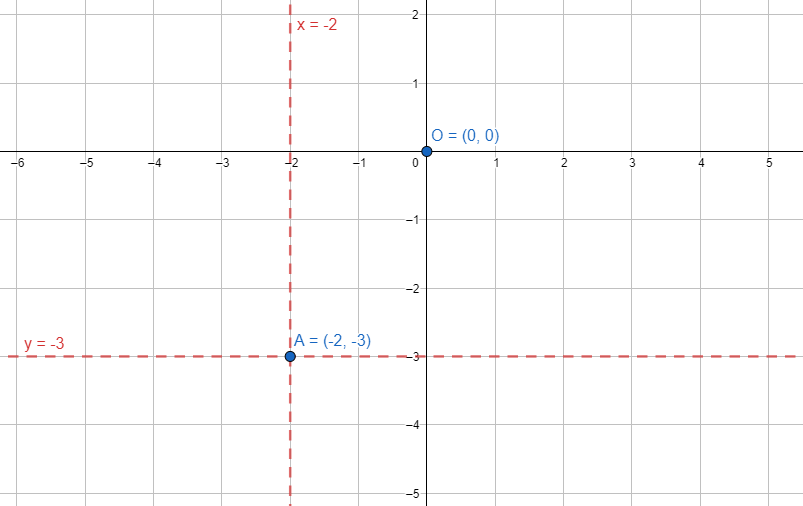
For a fixed point $ \left( a,b \right) $ in the previous position of the graph changes to $ \left( c,d \right) $ .
Then we can say $ c=a+2 $ and $ d=b+3 $ . This gives $ a=c-2 $ and $ b=d-3 $ .
Now point $ \left( a,b \right) $ satisfies $ {{x}^{2}}+{{y}^{2}}=49 $ . Putting the values, we get $ {{a}^{2}}+{{b}^{2}}=49 $ .
Now we replace the values and get $ {{\left( c-2 \right)}^{2}}+{{\left( d-3 \right)}^{2}}=49 $ .
Solving the equation, we get $ {{c}^{2}}-4c+{{d}^{2}}-6d=36 $ .
Now to get general equation we replace with $ \left( x,y \right) $ and get $ {{x}^{2}}+{{y}^{2}}-4x-6y=36 $ .
Therefore, the shifted equation is $ {{x}^{2}}+{{y}^{2}}-4x-6y=36 $ .

Note:
 The shift in the graph only changes the position of the origin which was $ \left( 0,0 \right) $. No change in the unit value of the graph for both coordinates happen. So, the change of coordinates will be always the addition or subtraction of constants.