Question

Find the ratio in which the point \[(2,y)\] divides the line segment joining the points \[A( - 2,2)\] and \[B(3,7)\]. Also, find the value of \[{\mathbf{y}}\].

Answer 1

Hint: To solve the question first we assume any variable as an alternative of the ratio to be found out. Then we must use the section formula to obtain the coordinate of the point that divides the line segment. Lastly, by comparing the abscissa and ordinate with the actual point that is \[\left( {2,y} \right)\], the values of variables under assumption can be determined and also the value of y.

Complete step-by-step solution:
We know the section formulae that the coordinate of a point that divides the line segment joining the points \[({x_1},{y_1})\] and \[({x_2},{y_2})\] in the ratio \[m:n\] is \[\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)\].

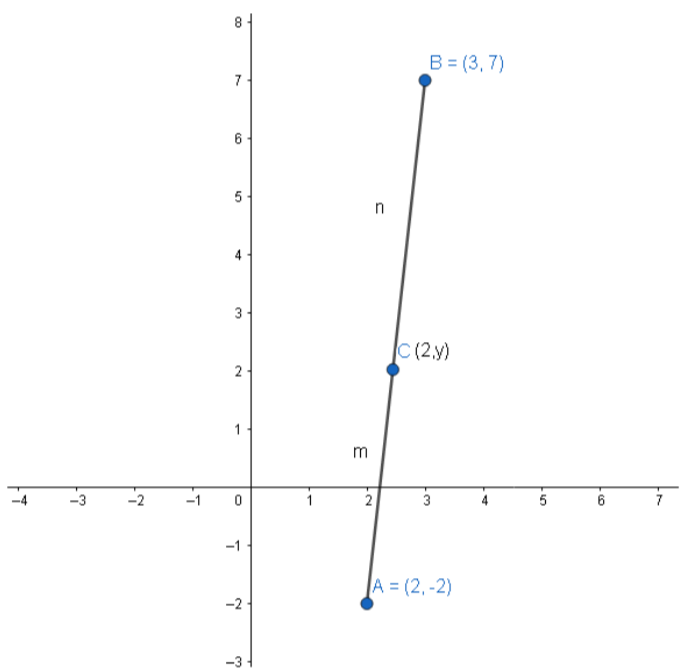
Consider the point C \[\left( {2,y} \right)\] divides the line segment joining the points \[\left( { - 2,2} \right)\] and \[\left( {3,7} \right)\] in the ratio\[m:n\]. Then by applying section formula the coordinate of C is given by
\[\left( {\dfrac{{3m - 2n}}{{m + n}},\dfrac{{7m + 2n}}{{m + n}}} \right)\].
But here the point is\[\left( {2,y} \right)\]. To find out the ratio or to find out the values of m and n we must compare the respective abscissa of the coordinates, and then we have
\[ \Rightarrow \dfrac{{3m - 2n}}{{m + n}} = 2 \\
   \Rightarrow 3m - 2n = 2(m + n) \\
   \Rightarrow 3m - 2m = 2n + 2n \\
   \Rightarrow m = 4n \\
   \Rightarrow m:n = 4:1 \]
Here we got the ratio is \[4:1\] that means \[m = 4\] and \[n = 1\].
To find out the value of y we must compare the ordinates that means \[\dfrac{{7m + 2n}}{{m + n}}\] with y and substituting the ratio values that is m=4 and n=1. Now we get,
\[y = \dfrac{{7 \times 4 + 2 \times 1}}{{4 + 1}} = 6\]
Here we got the value of \[y = 6\].

Note: If the point divides the line segment joining the points \[({x_1},{y_1})\] and \[({x_2},{y_2})\] externally with ratio \[m:n\] that means the point do not lie within the line segment. Then the coordinate of the point is given by \[\left( {\dfrac{{m{x_2} - n{x_1}}}{{m - n}},\dfrac{{m{y_2} - n{y_1}}}{{m - n}}} \right)\] for \[m > n\]. In alternative method the question can be solved by assuming the ratio as \[k:1\] instead of \[m:n\].