Question

Find the range of the function $f(x) = |x - 3|$.
A) $[2,10]$
B) $[2,8]$
C) $[0,\infty )$
D) $\mathbb{R}$

Answer 1

Hint: We will first get to know what the range of a function is. After that we will eliminate the obvious options and see for the rest of options by founding some counterexamples to discard them.

Complete step-by-step answer:
Let us first discuss what the range of a function is.
Range of a function is defined as the set of all output values of a function. The range of a function is the set of output values, or y-values, the function will give you when each value in the domain is input into the function. These, together, comprise the dependent variable.
We have with us a modulus function.
We know that modulus function is always positive because if $f(x) = |x - 3|$, then $f(x) = \left\{ {\begin{array}{*{20}{c}}
  { - x + 3,x < 3} \\
  {0,x = 3} \\
  {x - 3,x > 3}
\end{array}} \right.$.
Due to this kind of definition of modulus function, it can never be negative.
So, we cannot have any negative value in our Range.
Hence, $\mathbb{R}$ is eliminated.
Now, we are left with three options (A), (B) and (C).
We will pick up the largest interval among the options left with us and if that is the possible value, we will be done. Otherwise we will pick up the next biggest interval.
Here, the biggest one is $[0,\infty )$.
We can clearly see that if we put in the value of $x$ as 3 in $f(x) = |x - 3|$. We will get:-
$f(3) = |3 - 3| = |0| = 0$ and it can clearly go up to infinity because we can put in however large a value of $x$.

Hence, the correct option is (C).

Note: The students may think that we need to find the maximum. But if that would have been the case, (D) would have been the answer. We need to find the biggest interval which our function can cover.
The students can also look at the solution using graphs.
The graph of $f(x) = |x - 3|$ will be like as follows:-

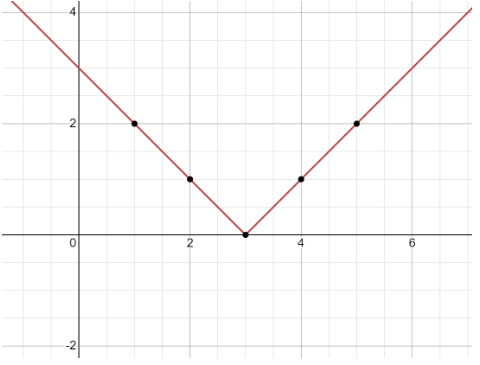
We can also clearly see here that function can take any value starting from 0 to infinity.