
Find the position vector of the a point lying on the line joining the points whose position vectors are $\hat{i}+\hat{j}-\hat{k}$ and $\hat{i}-\hat{j}+\hat{k}$. \[\]
Answer
579.9k+ views
Hint: We recall the definition of position vectors. We use the fact that the position vector of any point P that lies on the line joining two points A,B whose positions vector are known as $\overrightarrow{a},\overrightarrow{b}$ is given by $\overrightarrow{a}+\lambda \overrightarrow{d}$ where $\lambda $ is any real scalar and $\overrightarrow{d}=\overrightarrow{b}-\overrightarrow{a}$ is the distance vector.\[\]
Complete step by step answer:
We can represent any point in the space $P\left( x,y,z \right)$ as vector with original O as the initial point and P as the final point in terms of orthogonal unit vectors $\hat{i}$,$\hat{j}$ and $\hat{k}$ as $\overrightarrow{OP}=\overrightarrow{p}=x\hat{i}+y\hat{j}+\hat{k}$. This vector is called position vector, location vector or radius vector. We have the rough figure of the position vector $\overrightarrow{p}$ below. \[\]
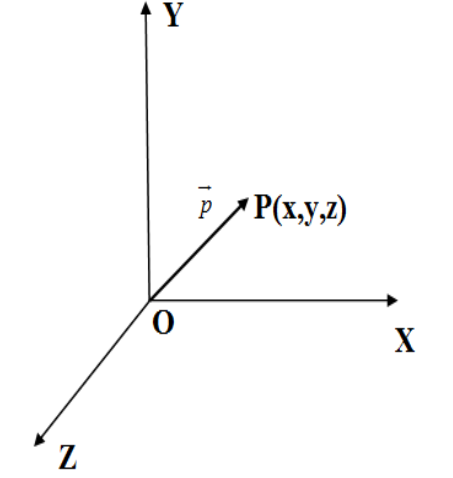
If there are $\overrightarrow{a}=\left( {{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k} \right),\overrightarrow{b}=\left( {{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k} \right)$ be two position vectors of two points then the position vector of any point on the line joining the two points is given with a real scalar $\lambda $as;
\[\begin{align}
& \overrightarrow{p}=\overrightarrow{a}+\lambda \overrightarrow{d} \\
& \Rightarrow \overrightarrow{p}=\overrightarrow{a}+\lambda \left( \overrightarrow{b}-\overrightarrow{a} \right) \\
& \Rightarrow \overrightarrow{p}=\left( {{a}_{1}}+\lambda \left( {{b}_{1}}-{{a}_{1}} \right) \right)\hat{i}+\left( {{a}_{2}}+\lambda {{b}_{2}}-{{a}_{2}} \right)\hat{j}+\left( {{a}_{3}}+\lambda \left( {{b}_{3}}-{{a}_{3}} \right) \right)\hat{k} \\
\end{align}\]
We are given in the question the position vectors of two points as $\hat{i}+\hat{j}-\hat{k}$ and $\hat{i}-\hat{j}+\hat{k}$. Let us denote the two points as A and B and the position vectors as $\overrightarrow{a}=\hat{i}+\hat{j}-\hat{k}$ and $\overrightarrow{b}=\hat{i}-\hat{j}+\hat{k}$.So we have
\[\begin{align}
& \overrightarrow{a}=\left( {{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k} \right)=\hat{i}+\hat{j}-\hat{k} \\
& \overrightarrow{b}=\left( {{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k} \right)=\hat{i}-\hat{j}+\hat{k} \\
\end{align}\]
We compare the respective components and we get;
\[\begin{align}
& \Rightarrow {{a}_{1}}=1,{{a}_{2}}=1,{{a}_{3}}=-1 \\
& \Rightarrow {{b}_{1}}=1,{{b}_{2}}=-1,{{b}_{3}}=1 \\
\end{align}\]
Let P be any point on the line segment joining A and B.The position vector of P is;
\[\begin{align}
& \overrightarrow{p}=\overrightarrow{a}+\lambda \overrightarrow{b}=\left( {{a}_{1}}+\lambda \left( {{b}_{1}}-{{a}_{1}} \right) \right)\hat{i}+\left( {{a}_{2}}+\lambda \left( {{b}_{2}}-{{a}_{2}} \right) \right)\hat{j}+\left( {{a}_{3}}+\lambda \left( {{b}_{3}}-{{a}_{3}} \right) \right)\hat{k} \\
& \Rightarrow \overrightarrow{p}=\left( 1+\lambda \cdot 0 \right)\hat{i}+\left( 1+\lambda \left( -2 \right) \right)\hat{j}+\left( -1+\lambda \cdot 2 \right)\hat{k} \\
& \Rightarrow \overrightarrow{p}=\hat{i}+\left( 1-2\lambda \right)\hat{j}+\left( -1+2\lambda \right)\hat{k} \\
\end{align}\]
Note: We also know that $\hat{i}$,$\hat{j}$ and $\hat{k}$ are orthogonal unit vectors (vectors with magnitude 1) along $x,y$ and $z$ axes respectively. If we want to find the position vector of midpoint , it is is given by $\dfrac{\overrightarrow{a}+\overrightarrow{b}}{2}$ and the position vector of any point that divides the line segment AB at a ratio $m:n$ is given by $\dfrac{m\overrightarrow{a}+n\overrightarrow{b}}{m+n}$. We note that the position vector of the point system reference is unique.
Complete step by step answer:
We can represent any point in the space $P\left( x,y,z \right)$ as vector with original O as the initial point and P as the final point in terms of orthogonal unit vectors $\hat{i}$,$\hat{j}$ and $\hat{k}$ as $\overrightarrow{OP}=\overrightarrow{p}=x\hat{i}+y\hat{j}+\hat{k}$. This vector is called position vector, location vector or radius vector. We have the rough figure of the position vector $\overrightarrow{p}$ below. \[\]
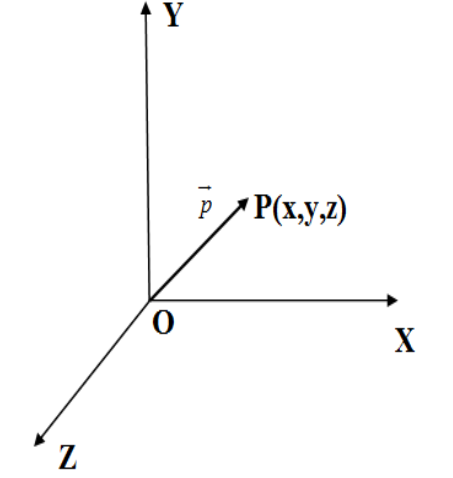
If there are $\overrightarrow{a}=\left( {{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k} \right),\overrightarrow{b}=\left( {{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k} \right)$ be two position vectors of two points then the position vector of any point on the line joining the two points is given with a real scalar $\lambda $as;
\[\begin{align}
& \overrightarrow{p}=\overrightarrow{a}+\lambda \overrightarrow{d} \\
& \Rightarrow \overrightarrow{p}=\overrightarrow{a}+\lambda \left( \overrightarrow{b}-\overrightarrow{a} \right) \\
& \Rightarrow \overrightarrow{p}=\left( {{a}_{1}}+\lambda \left( {{b}_{1}}-{{a}_{1}} \right) \right)\hat{i}+\left( {{a}_{2}}+\lambda {{b}_{2}}-{{a}_{2}} \right)\hat{j}+\left( {{a}_{3}}+\lambda \left( {{b}_{3}}-{{a}_{3}} \right) \right)\hat{k} \\
\end{align}\]
We are given in the question the position vectors of two points as $\hat{i}+\hat{j}-\hat{k}$ and $\hat{i}-\hat{j}+\hat{k}$. Let us denote the two points as A and B and the position vectors as $\overrightarrow{a}=\hat{i}+\hat{j}-\hat{k}$ and $\overrightarrow{b}=\hat{i}-\hat{j}+\hat{k}$.So we have
\[\begin{align}
& \overrightarrow{a}=\left( {{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k} \right)=\hat{i}+\hat{j}-\hat{k} \\
& \overrightarrow{b}=\left( {{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k} \right)=\hat{i}-\hat{j}+\hat{k} \\
\end{align}\]
We compare the respective components and we get;
\[\begin{align}
& \Rightarrow {{a}_{1}}=1,{{a}_{2}}=1,{{a}_{3}}=-1 \\
& \Rightarrow {{b}_{1}}=1,{{b}_{2}}=-1,{{b}_{3}}=1 \\
\end{align}\]
Let P be any point on the line segment joining A and B.The position vector of P is;
\[\begin{align}
& \overrightarrow{p}=\overrightarrow{a}+\lambda \overrightarrow{b}=\left( {{a}_{1}}+\lambda \left( {{b}_{1}}-{{a}_{1}} \right) \right)\hat{i}+\left( {{a}_{2}}+\lambda \left( {{b}_{2}}-{{a}_{2}} \right) \right)\hat{j}+\left( {{a}_{3}}+\lambda \left( {{b}_{3}}-{{a}_{3}} \right) \right)\hat{k} \\
& \Rightarrow \overrightarrow{p}=\left( 1+\lambda \cdot 0 \right)\hat{i}+\left( 1+\lambda \left( -2 \right) \right)\hat{j}+\left( -1+\lambda \cdot 2 \right)\hat{k} \\
& \Rightarrow \overrightarrow{p}=\hat{i}+\left( 1-2\lambda \right)\hat{j}+\left( -1+2\lambda \right)\hat{k} \\
\end{align}\]
Note: We also know that $\hat{i}$,$\hat{j}$ and $\hat{k}$ are orthogonal unit vectors (vectors with magnitude 1) along $x,y$ and $z$ axes respectively. If we want to find the position vector of midpoint , it is is given by $\dfrac{\overrightarrow{a}+\overrightarrow{b}}{2}$ and the position vector of any point that divides the line segment AB at a ratio $m:n$ is given by $\dfrac{m\overrightarrow{a}+n\overrightarrow{b}}{m+n}$. We note that the position vector of the point system reference is unique.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Giving reasons state the signs positive or negative class 12 physics CBSE

Explain esterification reaction with the help of a class 12 chemistry CBSE

What is defined as a solenoid Depict a diagram with class 12 physics CBSE




