Question

Find the position of nodes and antinodes
$\begin{align}
  & \text{A}\text{. }{{x}_{nodes}}=n\dfrac{\lambda }{3}\left( \dfrac{\pi }{6.0} \right)cm,\left( n=1,2,3..... \right);{{x}_{antinodes}}=n\left( \dfrac{\pi }{6.0} \right)cm,\left( n=1,3,5..... \right) \\
 & \text{B}\text{. }{{x}_{nodes}}=n\dfrac{\lambda }{3}\left( \dfrac{\pi }{3.0} \right)cm,\left( n=1,2,3..... \right);{{x}_{antinodes}}=n\left( \dfrac{\pi }{3.0} \right)cm,\left( n=1,3,5..... \right) \\
 & \text{C}\text{. }{{x}_{nodes}}=n\dfrac{\lambda }{2}\left( \dfrac{\pi }{3.0} \right)cm,\left( n=1,2,3..... \right);{{x}_{antinodes}}=n\left( \dfrac{\pi }{6.0} \right)cm,\left( n=1,3,5..... \right) \\
 & \text{D}\text{. }{{x}_{nodes}}=n\dfrac{\lambda }{2}\left( \dfrac{\pi }{6.0} \right)cm,\left( n=1,2,3..... \right);{{x}_{antinodes}}=n\left( \dfrac{\pi }{6.0} \right)cm,\left( n=1,3,5..... \right) \\
\end{align}$

Answer 1

Hint: A node is a point along with a standing wave where the amplitude of the wave is minimum. For example, the two ends of a string vibrating is the node. At the point of the node, the particle of the standing wave does not vibrate. The opposite of the node is anti-node, so anti-node is a point where the amplitude of the standing wave is maximum. First, write down the wave equation of a stationary wave or standing wave. From that wave equation calculate the condition for which the amplitude is maximum and minimum which will give the conditions for nodes and anti-nodes. Compare that condition with the options to get the correct answer.
Formulas used: The equation of a wave is given by
$y=A\sin \left( \omega t-kx \right)$ and
$k=\dfrac{2\pi }{\lambda }$

Complete step-by-step solution:
First, we have to create a standing wave and see what will be the positions of nodes and anti-nodes.
Consider two sinusoidal waves of equal amplitude and frequency travelling along a long string in opposite directions. The wave travelling along positive X-direction can be represented as
${{y}_{1}}=A\sin \left( \omega t-kx \right)$
The wave travelling along negative X-direction can be represented as
${{y}_{1}}=A\sin \left( \omega t+kx \right)$
According to the principle of superposition, the resultant wave is given by
$\begin{align}
  & y={{y}_{1}}+{{y}_{2}} \\
 & =A\sin \left( \omega t-kx \right)+A\sin \left( \omega t+kx \right) \\
 & =2A\sin \omega t.\cos kx[\because \sin (A+B)+\sin (A-B)=2\sin A.\cos B] \\
 & \Rightarrow y=\left( 2A\cos kx \right)\sin \omega t \\
\end{align}$
This equation represents a stationary wave. It cannot represent a progressive wave because the argument of any of its trigonometric functions does not contain the combination $\left( \omega t\pm kx \right)$. The stationary wave has the same angular frequency $\omega$ but has amplitude
 $A'=2A\cos kx$
Obviously in case of a stationary wave, the amplitude of oscillation is not same for all the particles. It varies harmonically with the location $x$ of the particle.
The amplitude will be zero at points, where
$\begin{align}
  & \cos kx=0 \\
 & or,kx=\left( n+\dfrac{1}{2} \right)\pi ,\text{ where }n=0,1,2,3... \\
 & or,\dfrac{2\pi x}{\lambda }=\left( n+\dfrac{1}{2} \right)\pi \left[ \because k=\dfrac{2\pi }{\lambda },\lambda =\text{wave length} \right] \\
 & or,x=\left( 2n+1 \right)\dfrac{\lambda }{4} \\
 & or,x=\dfrac{\lambda }{4},\dfrac{3\lambda }{4},\dfrac{5\lambda }{4},..... \\
\end{align}$
These positions of zero amplitude are called nodes. Clearly, the separation between two consecutive nodes is $\dfrac{\lambda }{4}$ .
The amplitude will have a maximum value of $2A$ at points, where
\[\begin{align}
  & \cos kx=\pm 1 \\
 & or,kx=n\pi ,\text{ where }n=0,1,2,3,...... \\
 & or,\dfrac{2\pi }{\lambda }x=n\pi \\
 & or,x=n\dfrac{\lambda }{2} \\
 & or,x=0,\dfrac{\lambda }{2},\lambda ,\dfrac{3\lambda }{2},2\lambda ,..... \\
\end{align}\]
These positions of maximum amplitude are called antinodes. Clearly, the antinodes are separated by \[\dfrac{\lambda }{2}\] and are located half way between pairs of nodes.

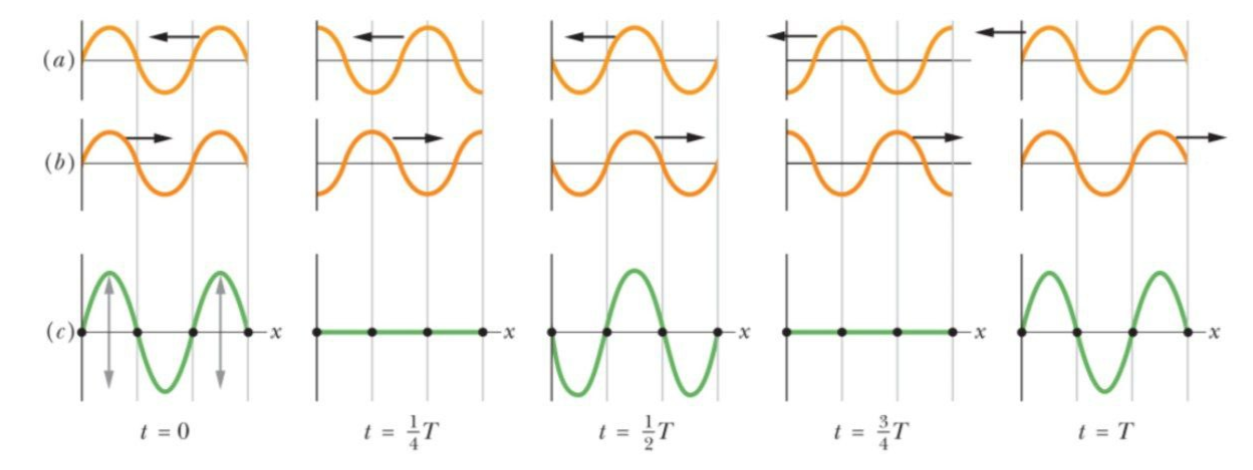
The figure represents five instants of the wave. The figure (a) and figure(b) represent the two identical wave. And figure (c) represents the resultant of the wave (a) and wave (b).
At $t=0,\dfrac{1}{2}T\text{ and }T$, fully constructive interference occurs because of the alignment of peaks with peaks and valleys with valleys. At $t=\dfrac{1}{4}T\text{ and }\dfrac{3}{4}T$fully destructive interference occurs because of the alignment of peaks with valleys. The nodes are marked with dots that will never oscillate and the antinodes are the points, which oscillate the most.

So the anti-nodes are situated at the exact midpoint of the nodes. From the options only option, only option C satisfies this condition. So the correct option is C.

Note: The changes of the wave with the time
At the instants $t=0,\dfrac{T}{2,},\dfrac{3T}{2},......$ we have
$\sin \omega t=\sin \dfrac{2\pi }{T}t=0$
Thus at these instants the displacement $y$ becomes zero at all the points. That is, all the particles of the medium pass through their mean positions simultaneously twice in each cycle.
 At the instants $t=\dfrac{T}{4},\dfrac{3T}{4},\dfrac{5T}{4},...$ we have
$\sin \omega t=in\dfrac{2\pi }{T}t=\pm 1$
Thus at these instants the displacement $y$ is maximum at all the points and becomes alternately positive and negative. That is, all the particles of the medium pass through their positions of maximum displacements twice in each cycle.