
Find the polar coordinates where the Cartesian coordinates are \[\]
(i)$\left( \sqrt{2},\sqrt{2} \right)$\[\]
(ii)$\left( 0,\dfrac{1}{2} \right)$\[\]
(iii)$\left( \dfrac{-1}{\sqrt{2}},\dfrac{-1}{\sqrt{2}} \right)$\[\]
(iv)$\left( \dfrac{3}{2},\dfrac{3\sqrt{3}}{2} \right)$\[\]
(v) $\left( -3,0 \right)$\[\]
(v) $\left( -\sqrt{2},\sqrt{2} \right)$\[\]
Answer
571.8k+ views
Hint: We recall the definitions of the polar coordinates $\left( r,\theta \right)$and Cartesian coordinates $\left( x,y \right)$. We find $r$ as the distance between origin and the Cartesian point as $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$ and $\theta $ as the angle the ray joining the origin and the point makes with positive $x-$axis $\theta =\operatorname{atan}2\theta $ where $\operatorname{atan}2\left( y,x \right)$ represents argument inverse tangent function. \[\]
Complete step by step answer:
We know that Cartesian coordinate system the position of the any point on the plane is represented by an ordered pair $\left( x,y \right)$ where $x$is called abscissa and calculated as the distance of the point from $y-$axis and $y$ is called ordinate and calculated as the distance of the point from $x-$axis. If we denote the point as P then $\left( x,y \right)$ is Cartesian coordinate of the point P .\[\]
We also know that in the polar coordinate system every point is represented in the plane with an ordered pair $\left( r,\theta \right)$ where $r$ is the distance from a reference point (conventionally origin) and $\theta $ is the angle from a reference direction (conventionally positive direction of $x-$axis) . The reference point is called the pole and the reference direction is called the polar axis. \[\]
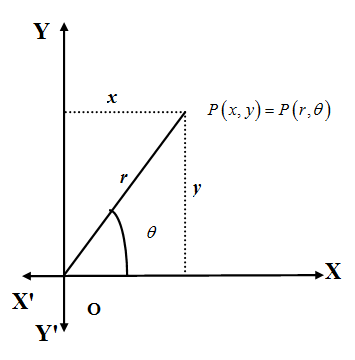
We can convert the Cartesian coordinate $\left( x,y \right)$ to polar coordinate $\left( r,\theta \right)$ of a point using the following relations
\[\begin{align}
& r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
& \theta =\operatorname{atan}2\left( y,x \right) \\
\end{align}\]
The function $\operatorname{atan}2\left( y,x \right)$ called 2-argument inverse tangent is defined as follows;
\[\theta =\left\{ \begin{matrix}
{{\tan }^{-1}}\left( \dfrac{y}{x} \right) & \text{if }x>0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)+\pi & \text{if }x<0\text{ and }y\ge 0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)-\pi & \text{if }x<0\text{ and }y<0 \\
\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
-\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
\text{undefined} & \text{if }x=0\text{ and }y=0 \\
\end{matrix} \right.\]
(i) We are given the Cartesian coordinates$\left( \sqrt{2},\sqrt{2} \right)$. So we have $x=\sqrt{2}>0,y=\sqrt{2}>0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( \sqrt{2} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}}=\sqrt{2+2}=\sqrt{4}=2 \\
& \theta ={{\tan }^{-1}}\dfrac{\sqrt{2}}{\sqrt{2}}={{\tan }^{-1}}1=\dfrac{\pi }{4} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 2,\dfrac{\pi }{4} \right)$\[\]
(ii) We are given the Cartesian coordinates$\left( 0,\dfrac{1}{2} \right)$. So we have $x=0,y=\dfrac{1}{2}>0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( \dfrac{1}{2} \right)}^{2}}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2} \\
& \theta =\dfrac{\pi }{2} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( \dfrac{1}{2},\dfrac{\pi }{2} \right)$\[\]
(iii) We are given the Cartesian coordinates$\left( \dfrac{-1}{\sqrt{2}},\dfrac{-1}{\sqrt{2}} \right)$. So we have $x=\dfrac{-1}{\sqrt{2}}<0,y=\dfrac{-1}{\sqrt{2}}<0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( \dfrac{-1}{\sqrt{2}} \right)}^{2}}+{{\left( \dfrac{-1}{\sqrt{2}} \right)}^{2}}}=\sqrt{\dfrac{1}{2}+\dfrac{1}{2}}=\sqrt{1}=1 \\
& \theta ={{\tan }^{-1}}\dfrac{\dfrac{-1}{\sqrt{2}}}{\dfrac{-1}{\sqrt{2}}}-\pi ={{\tan }^{-1}}1-\pi =\dfrac{\pi }{4}-\pi =\dfrac{-3\pi }{4} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 1,\dfrac{-3\pi }{4} \right)$\[\]
(iv) We are given the Cartesian coordinates$\left( \dfrac{3}{2},\dfrac{3\sqrt{3}}{2} \right)$. So we have $x=\dfrac{3}{2}>0,y=\dfrac{3\sqrt{3}}{2}>0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}+{{\left( \dfrac{3\sqrt{3}}{2} \right)}^{2}}}=\sqrt{\dfrac{9}{4}+\dfrac{27}{4}}=\sqrt{\dfrac{36}{4}}=\sqrt{9}=3 \\
& \theta ={{\tan }^{-1}}\dfrac{\dfrac{3\sqrt{3}}{2}}{\dfrac{3}{2}}={{\tan }^{-1}}\sqrt{3}=\dfrac{\pi }{3} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 3,\dfrac{\pi }{3} \right)$\[\]
(v) We are given the Cartesian coordinates$\left( -3,0 \right)$. So we have $x=-3<0,y=0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 0 \right)}^{2}}}=\sqrt{9}=3 \\
& \theta ={{\tan }^{-1}}\dfrac{0}{-3}+\pi ={{\tan }^{-1}}0+\pi =\pi \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 1,\pi \right)$\[\]
(vi) We are given the Cartesian coordinates$\left( -\sqrt{2},-\sqrt{2} \right)$. So we have $x=-\sqrt{2}<0,y=-\sqrt{2}<0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( -\sqrt{2} \right)}^{2}}+{{\left( -\sqrt{2} \right)}^{2}}}=\sqrt{2+2}=\sqrt{4}=2 \\
& \theta ={{\tan }^{-1}}\dfrac{-\sqrt{2}}{-\sqrt{2}}-\pi ={{\tan }^{-1}}1=\dfrac{\pi }{4}-\pi =\dfrac{-3\pi }{4} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 2,\dfrac{-3\pi }{4} \right)$\[\]
Note: We note that $r$(also called radial coordinate) is always positive and $\theta $(also called angular coordinate) is always measured in radian. The polar coordinate for origin does not exist. We can also convert the angle $\dfrac{-3\pi }{4}$to positive by adding $2\pi $. We can alternatively find $\theta $ with $x$ and $r$ as $\theta ={{\tan }^{-1}}\left( \dfrac{x}{r} \right)$ with the condition$y\ge 0,r\ne 0$, $\theta =-{{\tan }^{-1}}\left( \dfrac{x}{r} \right)$ with the condition $y<0$ and $\theta $ is undefined if $r=0$.
Complete step by step answer:
We know that Cartesian coordinate system the position of the any point on the plane is represented by an ordered pair $\left( x,y \right)$ where $x$is called abscissa and calculated as the distance of the point from $y-$axis and $y$ is called ordinate and calculated as the distance of the point from $x-$axis. If we denote the point as P then $\left( x,y \right)$ is Cartesian coordinate of the point P .\[\]
We also know that in the polar coordinate system every point is represented in the plane with an ordered pair $\left( r,\theta \right)$ where $r$ is the distance from a reference point (conventionally origin) and $\theta $ is the angle from a reference direction (conventionally positive direction of $x-$axis) . The reference point is called the pole and the reference direction is called the polar axis. \[\]
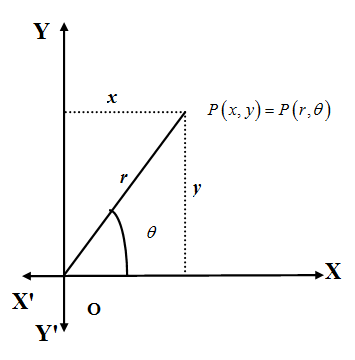
We can convert the Cartesian coordinate $\left( x,y \right)$ to polar coordinate $\left( r,\theta \right)$ of a point using the following relations
\[\begin{align}
& r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
& \theta =\operatorname{atan}2\left( y,x \right) \\
\end{align}\]
The function $\operatorname{atan}2\left( y,x \right)$ called 2-argument inverse tangent is defined as follows;
\[\theta =\left\{ \begin{matrix}
{{\tan }^{-1}}\left( \dfrac{y}{x} \right) & \text{if }x>0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)+\pi & \text{if }x<0\text{ and }y\ge 0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)-\pi & \text{if }x<0\text{ and }y<0 \\
\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
-\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
\text{undefined} & \text{if }x=0\text{ and }y=0 \\
\end{matrix} \right.\]
(i) We are given the Cartesian coordinates$\left( \sqrt{2},\sqrt{2} \right)$. So we have $x=\sqrt{2}>0,y=\sqrt{2}>0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( \sqrt{2} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}}=\sqrt{2+2}=\sqrt{4}=2 \\
& \theta ={{\tan }^{-1}}\dfrac{\sqrt{2}}{\sqrt{2}}={{\tan }^{-1}}1=\dfrac{\pi }{4} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 2,\dfrac{\pi }{4} \right)$\[\]
(ii) We are given the Cartesian coordinates$\left( 0,\dfrac{1}{2} \right)$. So we have $x=0,y=\dfrac{1}{2}>0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( \dfrac{1}{2} \right)}^{2}}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2} \\
& \theta =\dfrac{\pi }{2} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( \dfrac{1}{2},\dfrac{\pi }{2} \right)$\[\]
(iii) We are given the Cartesian coordinates$\left( \dfrac{-1}{\sqrt{2}},\dfrac{-1}{\sqrt{2}} \right)$. So we have $x=\dfrac{-1}{\sqrt{2}}<0,y=\dfrac{-1}{\sqrt{2}}<0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( \dfrac{-1}{\sqrt{2}} \right)}^{2}}+{{\left( \dfrac{-1}{\sqrt{2}} \right)}^{2}}}=\sqrt{\dfrac{1}{2}+\dfrac{1}{2}}=\sqrt{1}=1 \\
& \theta ={{\tan }^{-1}}\dfrac{\dfrac{-1}{\sqrt{2}}}{\dfrac{-1}{\sqrt{2}}}-\pi ={{\tan }^{-1}}1-\pi =\dfrac{\pi }{4}-\pi =\dfrac{-3\pi }{4} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 1,\dfrac{-3\pi }{4} \right)$\[\]
(iv) We are given the Cartesian coordinates$\left( \dfrac{3}{2},\dfrac{3\sqrt{3}}{2} \right)$. So we have $x=\dfrac{3}{2}>0,y=\dfrac{3\sqrt{3}}{2}>0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}+{{\left( \dfrac{3\sqrt{3}}{2} \right)}^{2}}}=\sqrt{\dfrac{9}{4}+\dfrac{27}{4}}=\sqrt{\dfrac{36}{4}}=\sqrt{9}=3 \\
& \theta ={{\tan }^{-1}}\dfrac{\dfrac{3\sqrt{3}}{2}}{\dfrac{3}{2}}={{\tan }^{-1}}\sqrt{3}=\dfrac{\pi }{3} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 3,\dfrac{\pi }{3} \right)$\[\]
(v) We are given the Cartesian coordinates$\left( -3,0 \right)$. So we have $x=-3<0,y=0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 0 \right)}^{2}}}=\sqrt{9}=3 \\
& \theta ={{\tan }^{-1}}\dfrac{0}{-3}+\pi ={{\tan }^{-1}}0+\pi =\pi \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 1,\pi \right)$\[\]
(vi) We are given the Cartesian coordinates$\left( -\sqrt{2},-\sqrt{2} \right)$. So we have $x=-\sqrt{2}<0,y=-\sqrt{2}<0$. Then we use conversion formula to have
\[\begin{align}
& r=\sqrt{{{\left( -\sqrt{2} \right)}^{2}}+{{\left( -\sqrt{2} \right)}^{2}}}=\sqrt{2+2}=\sqrt{4}=2 \\
& \theta ={{\tan }^{-1}}\dfrac{-\sqrt{2}}{-\sqrt{2}}-\pi ={{\tan }^{-1}}1=\dfrac{\pi }{4}-\pi =\dfrac{-3\pi }{4} \\
\end{align}\]
So the required polar coordinate is $\left( r,\theta \right)=\left( 2,\dfrac{-3\pi }{4} \right)$\[\]
Note: We note that $r$(also called radial coordinate) is always positive and $\theta $(also called angular coordinate) is always measured in radian. The polar coordinate for origin does not exist. We can also convert the angle $\dfrac{-3\pi }{4}$to positive by adding $2\pi $. We can alternatively find $\theta $ with $x$ and $r$ as $\theta ={{\tan }^{-1}}\left( \dfrac{x}{r} \right)$ with the condition$y\ge 0,r\ne 0$, $\theta =-{{\tan }^{-1}}\left( \dfrac{x}{r} \right)$ with the condition $y<0$ and $\theta $ is undefined if $r=0$.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




