Question

Find the perpendicular distance of the point $A\left( 5,11 \right)$ from the y-axis?
(a) 5
(b) 11

Answer 1

Hint:We start solving the problem by drawing all the information given in the problem. We then recall the equation of the y-axis and the fact that the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $ax+by+c=0$ is \[\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]. We now substitute the point given and use the equation of the y-axis in the formula. We make necessary calculations to get the desired result.

Complete step by step answer:
According to the problem, we need to find the perpendicular distance of the point $A\left( 5,11 \right)$ from the x-axis.
Let us draw the diagram to represent the situation.

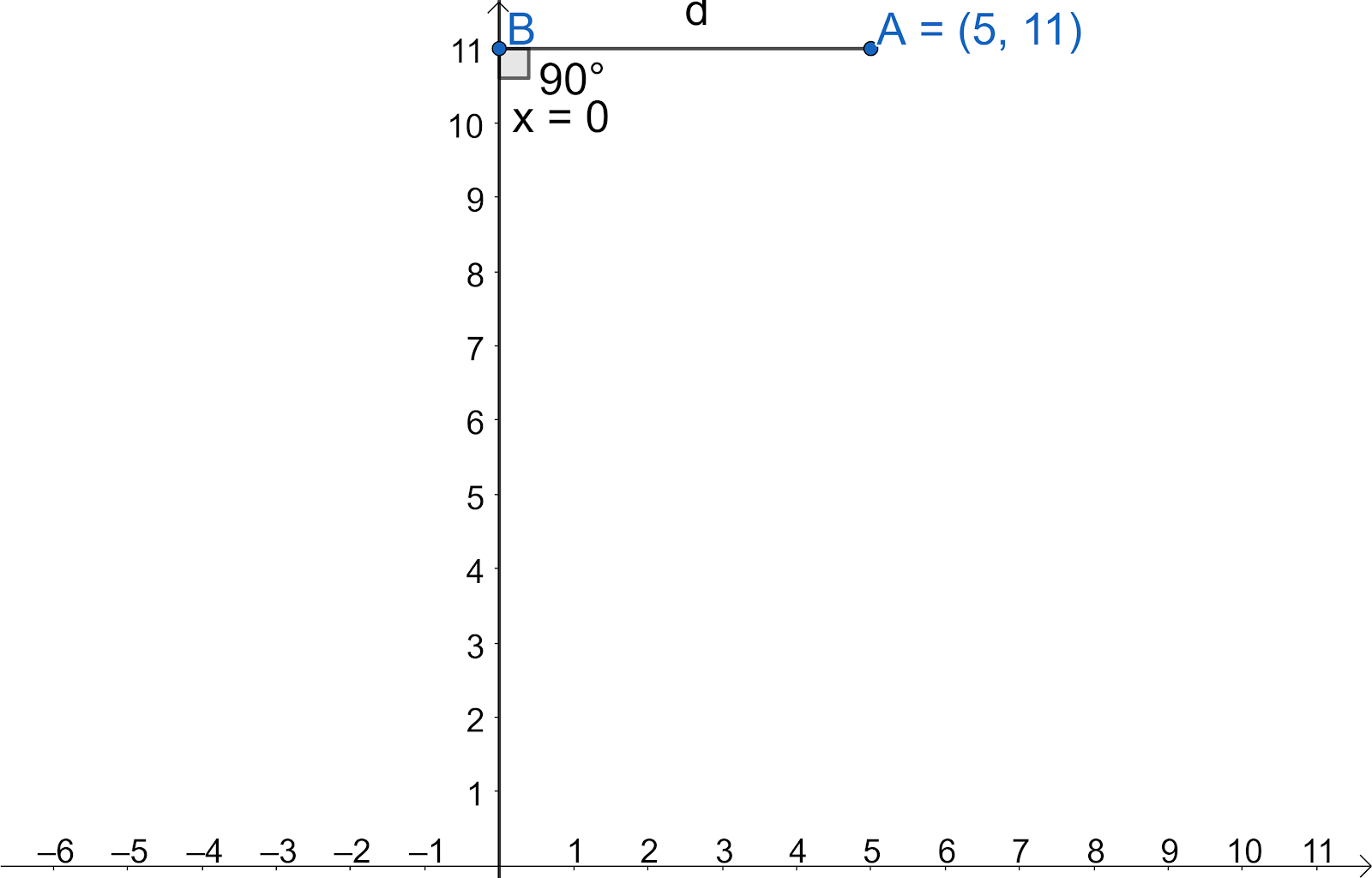
We know that the equation of the y-axis is $x=0$. Let us recall the definition of perpendicular distance between the point and a line.
We know that the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $ax+by+c=0$ is \[\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\].
Using this concept, we find the perpendicular between the point $\left( 5,11 \right)$ and the line $x=0$. Let us assume the required perpendicular distance’.
$\Rightarrow d=\dfrac{\left| 5 \right|}{\sqrt{{{1}^{2}}}}$.
$\Rightarrow d=\dfrac{5}{1}$.
$\Rightarrow d=5$.
We have found the distance of the point $\left( 5,11 \right)$ from y-axis as 5 units.
∴ The distance of the point $\left( 5,11 \right)$ from y-axis is 5 units.
The correct option for the given option is (a).

Note:
 We should not take negative values for the square root in the denominator while solving this problem, as the distance cannot be negative. We should make sure that whenever we apply modulus to any number, it gives us only a positive number or zero (only if the number is zero). We can alternatively solve the problem by finding the point B which was shown in the figure.
Since, the x-coordinate of the point on y-axis is 0 and we need to perpendicular distance from the point $A\left( 5,11 \right)$, the point B becomes $\left( 0,11 \right)$ as the points A and B lie on the line $y=11$.
We know that the distance two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
So, the perpendicular distance is distance between the points $A\left( 5,11 \right)$ and $B\left( 0,11 \right)$.
So, $d=\sqrt{{{\left( 0-5 \right)}^{2}}+{{\left( 11-11 \right)}^{2}}}$.
$\Rightarrow d=\sqrt{{{\left( -5 \right)}^{2}}+{{\left( 0 \right)}^{2}}}$.
$\Rightarrow d=\sqrt{25}$.
$\Rightarrow d=5$ units.