Question

How do you find the period of \[y=\csc \left( x-\dfrac{\pi }{2} \right)\]?

Answer 1

Hint: The graph of cosecant is unlike the graph of sine which is sinusoidal. So to find the period of cosecant in the given expression, we will directly compare the standard wave function to this given expression and calculate the required period of the cosecant. And since, the cosecant function does not have a waveform so it has no amplitude.

Complete step-by-step answer:
The graph of sine is a waveform like the sound or light waves, but when it comes to cosecant it is very likely not the case since, sine and cosecant are inverse of each other.
\[\sin \theta =\dfrac{1}{\csc \theta }\]
The graph of cosecant has no maxima or minima so it is not a sinusoidal like what we obtained for sine function. The graph of cosecant is as follows:

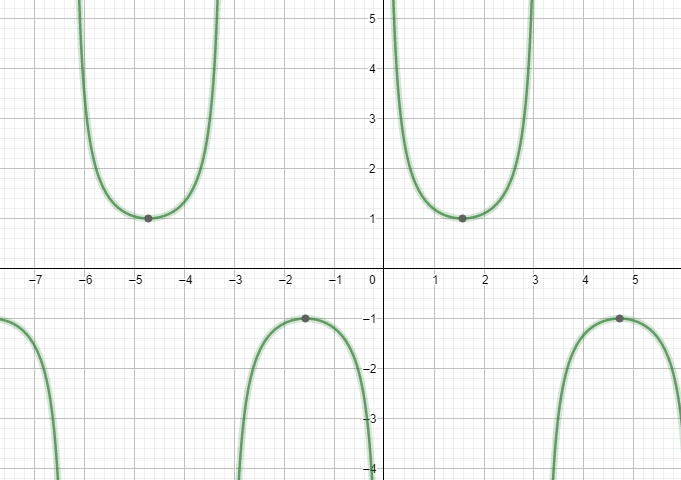
According to the question, we have to find the period of cosecant in the expression given, so we will use the formula of the wave function.
\[y=A\csc (B(x-C))+D\]
where A is the amplitude of the wave function which describes how high and how low the crest and troughs of the wave would be respectively
B denotes the cycles (or frequency) and is used in the expression of time period taken for one complete cycle
C refers to the horizontal displacement and D is the vertical displacement.
The expression given to us is: \[y=\csc \left( x-\dfrac{\pi }{2} \right)\]
On comparing, we get the values of the variables in the wave function, which are:
\[A=1\]
 \[B=1\]
\[C=\dfrac{\pi }{2}\]
\[D=0\]
Period of the function = \[\dfrac{2\pi }{|B|}\]
Substituting the value of B in the equation of period, we get,
 Period of the function
= \[\dfrac{2\pi }{|B|}\]
= \[\dfrac{2\pi }{|1|}=2\pi \]
From the graph of cosecant function, we can observe that the cosecant graph does not possess any maximum or minimum so if we were to calculate the amplitude of the given function as well it would be none.
Therefore, the period of \[y=\csc \left( x-\dfrac{\pi }{2} \right)\] is \[2\pi \].

Note: Cosecant function’s graph is unlike the sinusoidal graph we have for sine function so do not merge both the functions even though both are related, but remember they are inversely related and that makes all of the difference. While calculating the period, the value of B should be substituted correctly in the equation of period of a function.