Question

How do you find the period and graph the function \[y = 4\tan x\]?

Answer 1

Hint: We know that the distance between the repetitions of any function is called the period of the function.
For a trigonometric function, the length of one complete cycle is called a period.
If we have a function \[{\text{f}}\left( {\text{a}} \right) = {\text{tan}}\left( {{\text{as}}} \right)\], where \[s > 0\], then the graph of the function makes complete cycles between \[ - \dfrac{\pi }{2},0\] and \[0,\dfrac{\pi }{2}\] each of the function have the period of \[p = \dfrac{\pi }{s}\]
Substitute the value of \[s\], we can find the period.

Complete step-by-step solution:
It is given that; \[y = 4\tan x\]
We have to find the period and graph of the given function.
We know that the distance between the repetitions of any function is called the period of the function. For a trigonometric function, the length of one complete cycle is called a period.
If we have a function\[{\text{f}}\left( {\text{a}} \right){\text{ }} = {\text{ tan}}\left( {{\text{as}}} \right)\], where\[s > 0\], then the graph of the function makes complete cycles between \[ - \dfrac{\pi }{2},0\] and \[0,\dfrac{\pi }{2}\] each of the function have the period of \[p = \dfrac{\pi }{s}\]
Here, \[s = 4\]
So, the period of the given function \[y = 4\tan x\] is \[\dfrac{\pi }{4}\].
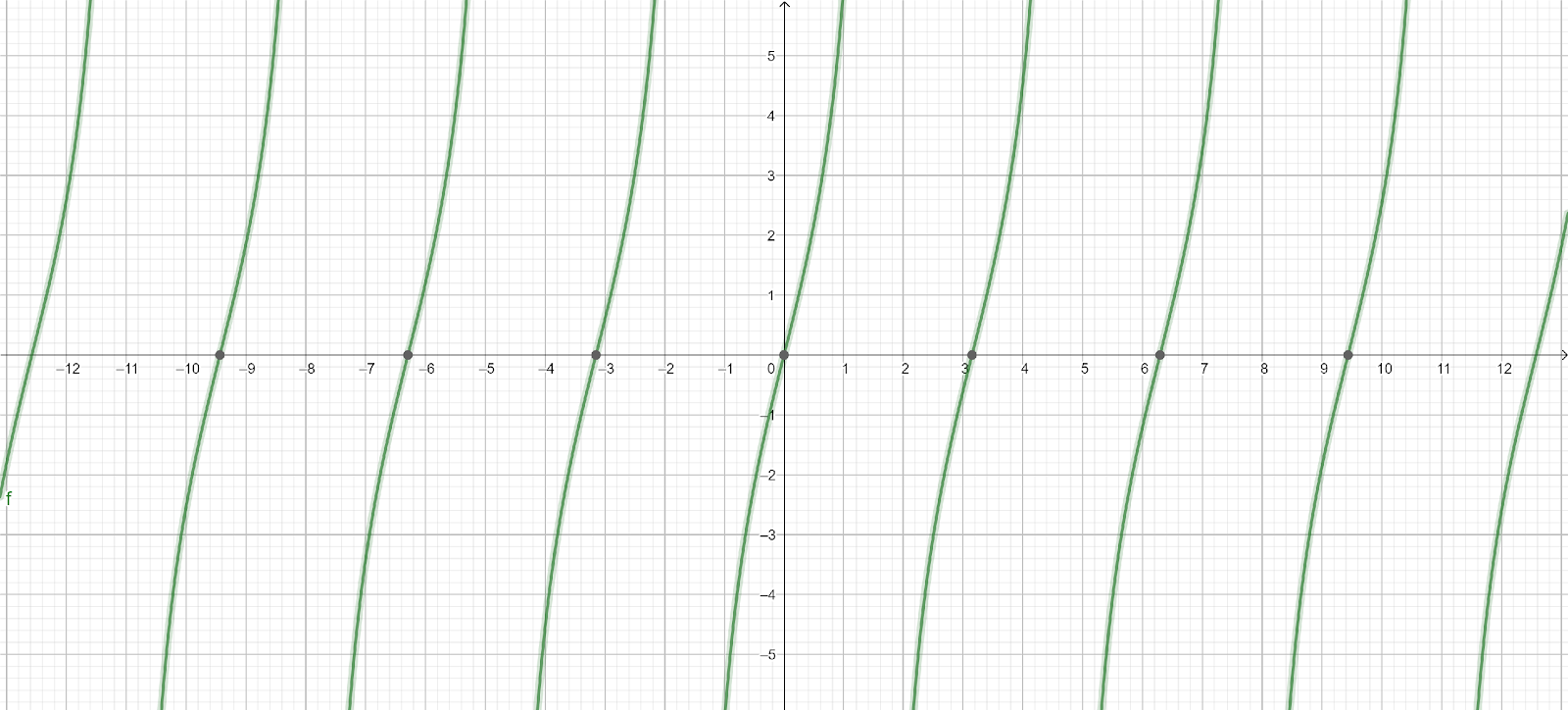
Answer, here’s the graph of \[y = 4\tan x\]

Note: The time interval between two waves is known as a Period whereas a function that repeats its values at regular intervals or periods is known as a Periodic Function. In other words, a periodic function is a function that repeats its values after every particular interval.
If a function repeats over at a constant period, we say that is a periodic function.
It is represented like \[f(x) = f(x + p)\], p is the real number and this is the period of the function.
Period means the time interval between the two occurrences of the wave.