Question

How do you find the perimeter and area of a right triangle if the shortest side is 9cm and the longest side is 15cm?

Answer 1

Hint: Here in this question, we have to find the perimeter of a right triangle of the given sides measure. As we know the perimeter of the triangle is the sum of all 3 sides measures. first we have to find the length of remaining one side of a right triangle by using the concept of Pythagoras theorem i.e., \[hy{p^2} = ad{j^2} + op{p^2}\] with the help of shortest and longest side of triangle and on further simplification to get the required result.

Complete step-by-step solution:
Finding the perimeter of a triangle means finding the distance around the triangle. The simplest way to find the perimeter of a triangle is to add up the length of all of its sides
The perimeter of the triangle with sides a, b and c is \[p = a + b + c\].
Consider a right triangle \[\Delta \,ABC\] where \[ B = {90^ \circ }\]

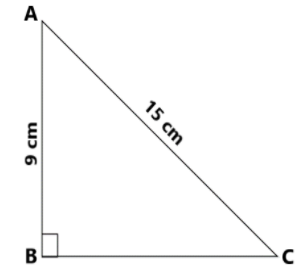
Remember, in a right triangle, the longest side is always the hypotenuse i.e., \[AC = 15\]cm
where x is the unknown side i.e.,\[BC = x\] and length of another side \[AB = 9\]cm
With this information, we can find the length of the unknown side, using Pythagorean Theorem,
\[hy{p^2} = ad{j^2} + op{p^2}\]
In \[\Delta \,ABC\] Pythagoras theorem can be written as
\[ \Rightarrow \,\,A{C^2} = A{B^2} + B{C^2}\]
On substituting the values, we get
\[ \Rightarrow \,\,{15^2} = {9^2} + {x^2}\]
\[ \Rightarrow \,\,{15^2} = {9^2} + {x^2}\]
\[ \Rightarrow \,\,225 = 81 + {x^2}\]
Subtract 81 on both side
\[ \Rightarrow \,\,225 - 81 = 81 + {x^2} - 81\]
\[ \Rightarrow \,\,144 = {x^2}\]
Or
\[ \Rightarrow \,\,{x^2} = 144\]
Taking square root on both side, then
\[ \Rightarrow \,\,x = \sqrt {144} \]
As we know 144 is the square number of 12, then
\[ \Rightarrow \,\,x = \sqrt {{{12}^2}} \]
On simplification, we get
\[ \Rightarrow \,\,x = 12\]
\[ \Rightarrow \,\,BC = 12\]cm
Perimeter of \[\Delta \,ABC\] is
\[P = 12 + 15 + 9\]
\[P = 36\]cm

Hence, the perimeter of the right triangle \[\Delta \,ABC\] is 36 cm.


Note: While determining the perimeter we use the formula. The unit for the perimeter will be the same as the unit of the length of a side or triangle. Whereas the unit for the area will be the square of the unit of the length of a triangle. We should not forget to write the unit. we should also know about the Pythagoras theorem.