Question

Find the number of points for which $ f\left( x \right)=\left\{ \begin{matrix}
   \max \left( \left| x \right|,{{x}^{2}} \right) & x<1 \\
   \min \left( 2x-1,{{x}^{2}} \right) & x\ge 1 \\
\end{matrix} \right. $ is not derivable. \[\]

Answer 1

Hint: We recall that the number of sharp turns or edges and discontinuities in the plot of the functions is the number of points where the function is not derivable. We equate the functions inside the minimum and maximum functions to find the points of a sharp turn. \[\]

Complete step by step answer:
We are given the following piecewise function.
\[f\left( x \right)=\left\{ \begin{matrix}
   \max \left( \left| x \right|,{{x}^{2}} \right) & x<1 \\
   \min \left( 2x-1,{{x}^{2}} \right) & x\ge 1 \\
\end{matrix} \right.\]
We see that We know that the absolute value function is not derivable at the point $ x=0 $ because of sharp turn and the point $ x=0 $ lie in the domain of $ \max \left( \left| x \right|,{{x}^{2}} \right) $ as $ x=0<1 $ . Let us equate the functions $ \left| x \right| $ and $ {{x}^{2}} $ to find the point where the function will show a sharp edge. From the definition absolute value function if $ x<0 $ we have;
\[\begin{align}
  & \left| x \right|={{x}^{2}} \\
 & \Rightarrow -x={{x}^{2}} \\
 & \Rightarrow {{x}^{2}}+x=0 \\
 & \Rightarrow x\left( x+1 \right)=0 \\
 & \Rightarrow x=0\text{ or }x=-1 \\
\end{align}\]
We have already established that at $ x=0 $ there will be a sharp turn. We use the definition of absolute value function and for $ 0\le x < 1 $ we have;
\[\begin{align}
  & \left| x \right|={{x}^{2}} \\
 & \Rightarrow x={{x}^{2}} \\
 & \Rightarrow {{x}^{2}}-x=0 \\
 & \Rightarrow x\left( x-1 \right)=0 \\
 & \Rightarrow x=0\text{ or }x=1 \\
\end{align}\]

We see that we are getting two more sharp edges at $ x=-1,1 $ since $ \left| x \right| > {{x}^{2}} $ for $ -1 < x < 1 $ and $ \left| x \right| < {{x}^{2}} $ for $ x < -1 $ and $ x > 1 $ but the function $ \max \left( \left| x \right|,{{x}^{2}} \right) $ is restricted to $ x < 1 $ . So we got two sharp edges at $ x=-1 $ and $ x=0 $ .
Let us check the minimum function $ \min \left( 2x-1,{{x}^{2}} \right) $ defined for all $ x\ge 1 $ . We equate $ 2x-1,{{x}^{2}} $ the find the sharp edges. We have
\[\begin{align}
  & 2x-1={{x}^{2}} \\
 & \Rightarrow {{x}^{2}}-2x+1=0 \\
 & \Rightarrow {{\left( x-1 \right)}^{2}}=0 \\
 & \Rightarrow x=1,1 \\
\end{align}\]
Since we are getting two equal roots, the function plot of $ 2x-1 $ will not cut but touch the plot of $ {{x}^{2}} $ at $ x=1 $ and we see that $ 2x-1 < {{x}^{2}} $ for all $ x > 1 $ . So we got So we can define the if the given function as;
\[f\left( x \right)=\left\{ \begin{matrix}
   {{x}^{2}} & x\le -1 \\
   -x & -1 < x < 0 \\
   x & 0\le x < 1 \\
   2x-1 & x\ge 1 \\
\end{matrix} \right.\]
We plot the above function in red and show three points of sharp edges occur below. \[\]

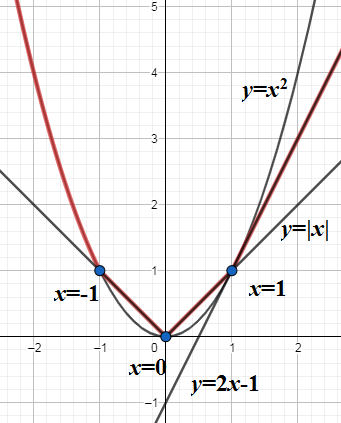
Note:
We should always remember that the function may be continuous at a point that may not differentiable at that point. A function has to be continuous at the nearest neighbourhood of that point to be differentiable. The function $ f\left( x \right)=\left| x \right| $ is continuous at $ x=0 $ but not differentiable at $ x=0 $ . Here in this problem at $ x=-1,1 $ is the function is through continuous but not differentiable. We can always find the left-hand derivative and right hand derivative to check differentiability.