Question

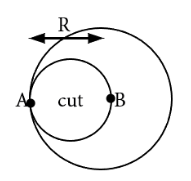
Find the moment of inertia of the circular disc of mass $ M $ and radius $ R $ cut as shown in figure below, about an axis through A and normal to the plane of the disc.

Answer 1

Hint : The total moment of inertia is the moment of inertia as though the hole hasn’t been there minus the moment of inertia if the hole had been a solid disk. The moment of inertia at an axis at the surface is equal to the moment of inertial at the centre plus the mass times the square of the radius of the disc.

Formula used: In this solution we will be using the following formula;
 $ \Rightarrow {I_d} = \dfrac{{M{R^2}}}{2} $ , where $ {I_d} $ , is the moment of inertia of a disc at an axis through its centre, $ M $ is the mass of the disc.
 $ \Rightarrow {I_s} = {I_c} + M{R^2} $ where $ {I_s} $ is the moment of inertia about an axis at the surface , and $ {I_c} $ is the moment of inertia about an axis through its centre.

Complete step by step answer
To calculate the moment of inertia, we first assume that the hole is absent. The moment of inertia through A would be given by
 $ \Rightarrow {I_A} = {I_B} + M{R^2} $ , where $ {I_A} $ is the moment of inertia about an axis through A the surface , and $ {I_B} $ is the moment of inertia about an axis through B, its centre, and $ M $ is the mass, $ R $ is the radius.
Hence,
 $ \Rightarrow {I_A} = \dfrac{{M{R^2}}}{2} + M{R^2} = \dfrac{3}{2}M{R^2} $ (since $ {I_d} = \dfrac{{M{R^2}}}{2} $ , where $ {I_d} $ , is the moment of inertia of a disc at an axis through its centre)
Now, we shall calculate the moment of inertia of the disk cutaway.
The disk has a radius of $ \dfrac{R}{2} $
Mass can be given as $ M = \sigma A = \sigma 2\pi {R^2} $ where $ \sigma $ is surface density.
Hence, for the cut disk $ {M_c} = \sigma A = \sigma 2\pi {\left( {\dfrac{R}{2}} \right)^2} $ .
 $ \Rightarrow {M_c} = \sigma 2\pi \dfrac{{{R^2}}}{4} = \dfrac{M}{4} $
Hence, Moment of inertia is given as
 $ \Rightarrow {I_{AC}} = \dfrac{1}{2}\left( {\dfrac{M}{4}{{\left( {\dfrac{R}{2}} \right)}^2}} \right) + \left( {\dfrac{M}{4}{{\left( {\dfrac{R}{2}} \right)}^2}} \right) $ , where $ {I_{AC}} $ is the moment of inertia of the cutaway disk at an axis through A.
Hence,
 $ \Rightarrow {I_{AC}} = \dfrac{3}{2}\left[ {\left( {\dfrac{M}{4}\dfrac{{{R^2}}}{4}} \right)} \right] = \dfrac{3}{{32}}M{R^2} $
Now, since the disc with radius $ \dfrac{R}{2} $ is actually removed then, we subtract it from the moment of inertia of the whole disk.
Thus,
 $ \Rightarrow {I_{A - AC}} = \dfrac{3}{2}M{R^2} - \dfrac{3}{{32}}M{R^2} $
Hence,
 $ \Rightarrow {I_{A - AC}} = \dfrac{3}{2}M{R^2}\left( {1 - \dfrac{1}{{16}}} \right) = \dfrac{3}{2}M{R^2} \times \dfrac{{15}}{{16}} $
 $ \Rightarrow {I_{A - AC}} = \dfrac{{45}}{{32}}M{R^2} $.

Note
For clarity, the reason why we can simply subtract the moment of inertia is because the moment of inertia of any body is simply the rotational equivalent of mass. Just like the end mass of the cut disk would have been the mass of the whole disk minus the mass of the cut disk. The end moment of inertia is simply that but with mass replaced with moment of inertia.