Question

How do you find the measure of the angles of an isosceles triangle if the measure of the vertex angle is \[40\] degrees less than the sum of the measures of the base angles?

Answer 1

Hint: This is one of the very simple problems of geometry. To solve this problem smoothly we first need to understand some of the properties of a triangle. The properties that we need to remember are:
1. The sum of all the angles of a triangle is \[180\] degrees.
2. In an isosceles triangle two sides are equal to one another and hence the opposite angles are also equal.

Complete step by step answer:
Keeping in mind the two properties and starting off with the solution we assume that the two angles which are equal to one another are equal to the value \[x\] degrees. Let us assume that the value of the third angle is equal to \[y\] degrees. Now according to the problem description, we can figure out a relation between \[x\] and \[y\] . The two base angles are equal to \[x\] degrees and the angle opposite to the base is \[y\] degrees. Thus, \[y=2x-40\] .

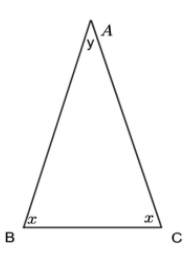
In the above figure, $ \Delta ABC $ is the isosceles triangle with $ A $ being the vertex angle, being equal to $ y $ and, $ B $ and $ C $ are the base angles, each being equal to $ x $.
Now according to the first property, we can write the sum of all the angles of a triangle is \[180\] degrees. Therefore, we can say,
\[x+x+y=180\]
Now, substituting the value of \[y\] as obtained above, we can rewrite the equation as,
\[x+x+2x-40=180\]
Now adding up the like terms, and rearranging them we can write,
\[\begin{align}
  & 4x=220 \\
 & \Rightarrow x=\dfrac{220}{4} \\
 & \Rightarrow x=55 \\
\end{align}\]
Thus, from this we can say that the base angles of the isosceles triangle are \[55\] degrees. The remaining angle is equal to \[y=2x-40\] ,
\[\begin{align}
  & y=2\left( 55 \right)-40 \\
 & \Rightarrow y=110-40 \\
 & \Rightarrow y=70 \\
\end{align}\]
Thus, all the three angles of the isosceles triangle are - \[55,55,70\] degrees.

Note:
We need to remember the properties of the triangles and then evaluate them to find all the required angles. In an equilateral triangle all the sides are equal and so are the angles. In a scalene triangle, none of the angles or sides are equal to one another.