Question

Find the length of the diagonal of a rectangle whose length is 15 cm and breadth is 8 cm.

Answer 1

Hint: To solve the given question, we will first find out what a rectangle is. After finding out, we will divide the rectangle by making a diagonal. Now, we will apply the Pythagoras theorem in the obtained right-angled triangle. The Pythagoras theorem says that, $$H^2=P^2+B^2$$ where H is the hypotenuse, B is the base and P is the perpendicular. We will put the value of the base and the perpendicular as the length and breadth of the rectangle and find out the value of the hypotenuse which is the diagonal of the given rectangle.

Complete step by step answer:
For a better understanding of the question, we will first find out what a rectangle is and then we will draw a rough sketch of the rectangle and a diagonal in it. A rectangle is a quadrilateral in which opposite sides are parallel and equal in length. The adjacent sides may be equal. The interior angle in the rectangle is $${90}^o.$$ A rough sketch of the rectangle is shown below.

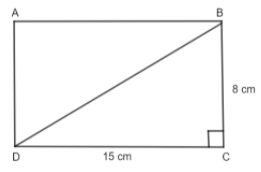
Here, AB = CD is the length of the rectangle and AD = BC is the breadth of the rectangle and BD is the diagonal. We can see that the triangle BCD is a right-angled triangle. So, here we will consider the right-angled triangle BCD. In this triangle, we will apply the Pythagoras theorem. The Pythagoras theorem says that the square of the hypotenuse (i.e. the side opposite to $${90}^o$$) is equal to the sum of the squares of the perpendicular and the base, i.e,
$$H^2=P^2+B^2$$
In our case, H = BD, B = CD and P = BC. On putting these values in the above formula, we will get,
$${\left(BD\right)}^2={\left(CD\right)}^2+{\left(BC\right)}^2$$
$$\Rightarrow {\left(BD\right)}^2={\left(15cm\right)}^2+{\left(8cm\right)}^2$$
$$\Rightarrow {\left(BD\right)}^2=225c{m}^2+64c{m}^2$$
$$\Rightarrow {\left(BD\right)}^2=289c{m}^2$$
$$\Rightarrow BD=\sqrt{289c{m}^2}$$
$$\Rightarrow BD=17cm$$
Thus, the length of the diagonal is 17 cm.

Note: We have calculated the length of the diagonal BD. Instead, we can also calculate the diagonal AC of the rectangle.

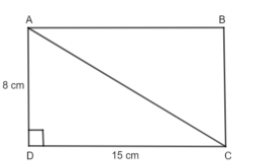
Now, we will apply the Pythagoras theorem in triangle ACD. Thus, we have,
$${\left(AC\right)}^2={\left(AD\right)}^2+{\left(DC\right)}^2$$
$$\Rightarrow {\left(AC\right)}^2={\left(8cm\right)}^2+{\left(15cm\right)}^2$$
$$\Rightarrow {\left(AC\right)}^2=289c{m}^2$$
$$\Rightarrow AC=17cm$$
Thus, the length of the diagonal AC is 17 cm and it is correct because the length of the diagonals AC and BD will be the same.