Question

Find the least value of sec A + sec B + sec C in acute angle triangle.

Answer 1

Hint: For solving this question we will use two theorems that are Carnot's theorem and Euler’s theorem. We will apply the basic trigonometric formulas and the fact that arithmetic sum is greater than or equal to geometric sum and solve accordingly.

Complete step-by-step solution -
The centre of a triangle is known as a circumcentre. It is where the perpendicular bisectors (lines that are at right angles to the midpoint of each side of a triangle) meet. The circumradius(R) of a cyclic polygon is the radius of the circumscribed circle of that polygon. For a triangle, it is the measure of the radius of the circle that circumscribes the triangle. Since every triangle is cyclic, every triangle has a circumscribed circle, or a circumcircle. The inradius(r) of a triangle is the radius of the incircle, which is the largest circle that will fit inside the triangle.

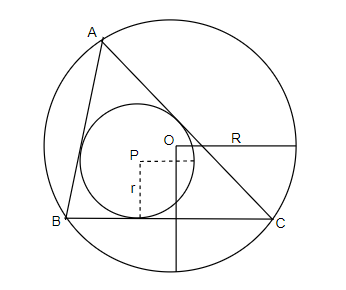
We know that, Carnot's theorem states that the sum of the distances from the circumcentre to the three sides of a triangle equals the sum of the circumradius(R) and the inradius(r),
Hence:
$\Rightarrow R(\cos A+\cos B+\cos C)=R+r$
$\Rightarrow \cos A+\cos B+\cos C=1+\dfrac{r}{R}$ \[\ldots ..\text{ }\left( 1 \right)\]
By Euler’s theorem we have,
$\Rightarrow R\ge 2r$
$\Rightarrow \dfrac{r}{R}\le \dfrac{1}{2}$ \[\ldots ..\text{ }\left( 2 \right)\]
Substituting equation (2) in equation (1), we get,
$\begin{align}
  & \Rightarrow \cos A+\cos B+\cos C=1+\dfrac{r}{R} \\
 & \Rightarrow \cos A+\cos B+\cos C\le 1+\dfrac{1}{2} \\
\end{align}$
Hence,
$\Rightarrow \cos A+\cos B+\cos C\le \dfrac{3}{2}$ \[\ldots ..\text{ }\left( 3 \right)\]
Now applying the fact that arithmetic mean is greater than equal to the geometric mean we have:
$\Rightarrow \text{A}\text{.M}\ge \text{G}\text{.M}$
$\Rightarrow \dfrac{\cos A+\cos B+\cos C}{3}\ge {{\left( \cos A\cdot \cos B\cdot \cos C \right)}^{\dfrac{1}{3}}}$ \[\ldots ..\text{ }\left( 4 \right)\]
Substituting equation (3) in equation (4) we get,
$\begin{align}
  & \Rightarrow \dfrac{3}{2}\times \dfrac{1}{3}\ge {{\left( \cos A\cdot \cos B\cdot \cos C \right)}^{\dfrac{1}{3}}} \\
 & \Rightarrow \dfrac{1}{2}\ge {{\left( \cos A\cdot \cos B\cdot \cos C \right)}^{\dfrac{1}{3}}} \\
\end{align}$
It gives,
$\begin{align}
  & \Rightarrow \cos A\cdot \cos B\cdot \cos C\le {{\left( \dfrac{1}{2} \right)}^{3}} \\
 & \Rightarrow \cos A\cdot \cos B\cdot \cos C\le \left( \dfrac{1}{8} \right) \\
\end{align}$
This means that:
$\begin{align}
  & \Rightarrow 8\le \dfrac{1}{\cos A\cdot \cos B\cdot \cos C} \\
 & \Rightarrow 8\le \sec A\cdot \sec B\cdot \sec C \\
\end{align}$
Again, applying the fact that arithmetic mean is greater than equal to the geometric mean we have:
$\Rightarrow {{\left( \sec A\cdot \sec B\cdot \sec C \right)}^{\dfrac{1}{3}}}\le \dfrac{\sec A+\sec B+\sec C}{3}$
$\begin{align}
  & \Rightarrow \dfrac{\sec A+\sec B+\sec C}{3}\ge {{8}^{\dfrac{1}{3}}} \\
 & \Rightarrow \dfrac{\sec A+\sec B+\sec C}{3}\ge 2 \\
\end{align}$
Hence,
$\Rightarrow \sec A+\sec B+\sec C\ge 6$
Hence, the least value of sec A + sec B + sec C in an acute angle triangle is 6.

Note: For solving this type of questions, we should know the concept of trigonometry. We should be aware of the basic facts of arithmetic progression and geometric progression. We should avoid any error related greater than or equal to sign.