Question

Find the least number which when divided by 15, leaves a remainder of 5, when divided by 25, leaves a remainder of 15 and when divided by 35 leaves a remainder of 25.
A.515
B.525
C.1040
D.1050

Answer 1

Hint: Here we will use the concept of the LCM. Firstly we will find the LCM of all the divisors i.e. 15, 25 and 35. Then we will see the pattern of getting the remainder by observing the difference between the divisor and the remainder. Then we will subtract the observed difference from the LCM of all the divisors to get the required value.

Complete step-by-step answer:
First, we will find the LCM of the divisors of the number i.e. 15, 25 and 35. Therefore, we get

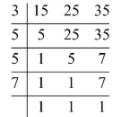
LCM of 15, 25 and 35 \[ = 3 \times 5 \times 5 \times 7 = 525\]
LCM of 15, 25 and 35 is equal to 525.
We know that when the divisor is 15 the remainder is 5, when the divisor is 25 the remainder is 15 and when the divisor is 35 the remainder of 25.
Now we can see that when the number is divided by the divisors then the remainder obtained is always 10 less than the divisor.
So, this means that the required number must be 10 less than the LCM of the divisors. Therefore, we get
Required number \[ = 525 - 10 = 515\]
Hence, the least number which satisfies the given condition is equal to 515.
So, option A is the correct option.

Note: Remainder is the value of the left over when a number is not exactly divisible by the other number. Zero is the remainder when a number exactly divides the other number.
In addition, we should know how to find the LCM (Least Common Multiple) of the numbers. LCM is the smallest positive integer that is divisible by the numbers. Here we should note that HCF is the short form of highest common factor which is the largest factor which is the largest common divisor of both the numbers.