Question

How do you find the least common multiple using prime factorisation?

Answer 1

Hint: It is a descriptive form of an answer. Here in this question, we have to write the detailed explanation of finding the least common multiple using prime factorisation. the factors will be in the form of prime numbers itself. We solve this question by considering the examples of numbers where prime factorisation involves.

Complete step-by-step solution:
Factorisation or factoring is defined as the breaking of a number into a product of other factors, which when multiplied together give the original number. A prime number is defined as the number which is divisible by the number 1 and the number by itself.
The prime factorisation involves the prime factors. When we want to determine the least common multiple by the prime factorisation method, we follow this procedure.
Consider the two numbers, find the prime factorization of each number and then write each number as a product of primes. If the prime factor is repeated for both the numbers then consider once and then multiply the factors then we obtain the LCM.
Let us consider one example.
Example: find the least common multiple for the numbers 12 and 9 by prime factorisation.
Now consider the numbers 12 and 9. let we factorise the number 12

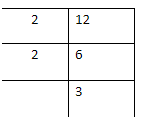
Therefore the number 12 is written as \[12 = 2 \times 2 \times 3\]
let we factorise the number 9

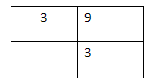
Therefore the number 9 is written as \[9 = 3 \times 3\]
The factors for both the numbers are the primes itself.
Now the LCM for the numbers 12 and 9 is, the number 3 is common for both the numbers so let us consider once while multiplying.
Therefore the LCM of 12 and 9 is \[2 \times 2 \times 3 \times 3 = 36\]
Hence LCM of 12 and 9 is 36.

Note: We must know about the multiplication, division and tables of multiplication to solve the question. We should divide the number by the least number and it should be a prime and hence it is the correct way to solve the problem. In prime factorisation the factors must and are in the form of primes.