Question

Find the LCM of the numbers \[6\] and \[5\]. Observe a common property in the obtained LCMs. Is LCM the product of two numbers?

Answer 1

Hint: LCM is elaborated as Least Common Multiple, which is the lowest common factor among the integers. To find the LCM of the given numbers, which is the lowest common number, which is divisible by all numbers for which we are finding the LCM, the method includes basic factorization of the numbers to find factors that are multiplied together to form a number. First, find the factors of the number that are the number when multiplied together gives the original number.
Co-prime numbers are those prime numbers whose only common multiple is 1. In Co-prime numbers, the factor of one number does not divide the other.

Complete step by step solution:
To find the lowest common multiple of the numbers, let’s find the factors of the given numbers for which we have to find the LCM of the numbers \[6\] and \[5\].
Factors are the integers, which, when multiplied together results in the original number only. First, find the factors of numbers

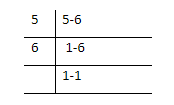
The unique common multiple of these numbers is \[1\].
Hence we can say the given numbers are co-prime as they have only a common multiple as\[1\].
Now multiply the common multiple with the other factors of the LCM
\[ = 1 \times \left[ {6 \times 5} \right] \\
   = 1 \times 30 \\
   = 30 \\ \]
Hence, the LCM of the numbers \[6\] and \[5\] is \[30\]
Yes, the product of the numbers is LCM as already proved the numbers to be Co-prime. Also, we can see \[6 \times 5 = 30\] which is equal to the LCM of these two numbers.

Note: If we are asked to add a number to make a number perfect square or perfect cube first we find the number which is a perfect square or perfect cube respectively nearest to it.