
Find the last two digits of ${17^{256}}$.
Answer
572.1k+ views
Hint: We will break $17$ into two parts ${(10 + 7)^{256}}$. Further we will use a binomial theorem formula to get the desired result.
Formula of binomial theorem: $p(x) = \dfrac{{n!}}{{(n - x)!x!}} \times {(p)^n}.{(q)^{n - x}}$
Complete step by step solution:
The given numbers: ${17^{256}}$
For finding the last two digits we have to find the remainder of ${17^{256}}$.
We will apply binomial expansion ${17^{256}}$.
${17^{256}} = {(10 + 7)^{256}}$.
\[{17^{256}} = {\,^{256}}{C_0}{10^0}{7^{256}} + {\,^{256}}{C_1}{10^1}{7^{256 - 1}}\]
${17^{256}} = {\,^{256}}{C_0}{10^0}{7^{256}} + {\,^{256}}{C_1}{10^1}{7^{255}}$
We will solve this value in two parts
So, ${I_1} = {\,^{256}}{C_0}{10^o}{7^{256}}$ and ${I_2} = $$^{256}{C_1}{10^1}{7^{255}}$
${I_1} = {\,^{256}}{C_0}{10^o}{7^{256}}$
We get last digit by last digit of ${\,^{256}}{C_0}{10^0}{7^{256}}$
We divide of $256$ by $4$
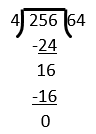
This number is divided completely, so
${7^0} = 1$
${I_1} = 1$
${I_2} = {\,^{256}}{C_1}{10^1}\,{7^{255}}$
$ = \dfrac{{256!}}{{256 - 1!1!}} \times {10^1} \times {7^{255}}$
$ = \dfrac{{256!}}{{255!1!}} \times {10^1} \times {7^{255}}$
$ = \dfrac{{256 \times 255!}}{{255!}} \times {10^1} \times {7^{255}}$
$ = 256 \times {10^1} \times {7^{253}}$
Now, we will complete the power of $255$
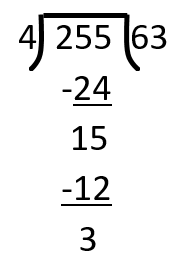
\[7 \times 7 \times 7 = 343\], we calculate last digit only
$6 \times 3 = 18$
Here last digit is also $8$
${17^{256}} = 81$
Note: Students should divide the powers of $17\,\,by\,\,4$. If the power is completely divided by $4$ then the answer will be given by ${7^4}$ and if the power is not completely divisible by $4$ then remainder will be left.
Formula of binomial theorem: $p(x) = \dfrac{{n!}}{{(n - x)!x!}} \times {(p)^n}.{(q)^{n - x}}$
Complete step by step solution:
The given numbers: ${17^{256}}$
For finding the last two digits we have to find the remainder of ${17^{256}}$.
We will apply binomial expansion ${17^{256}}$.
${17^{256}} = {(10 + 7)^{256}}$.
\[{17^{256}} = {\,^{256}}{C_0}{10^0}{7^{256}} + {\,^{256}}{C_1}{10^1}{7^{256 - 1}}\]
${17^{256}} = {\,^{256}}{C_0}{10^0}{7^{256}} + {\,^{256}}{C_1}{10^1}{7^{255}}$
We will solve this value in two parts
So, ${I_1} = {\,^{256}}{C_0}{10^o}{7^{256}}$ and ${I_2} = $$^{256}{C_1}{10^1}{7^{255}}$
${I_1} = {\,^{256}}{C_0}{10^o}{7^{256}}$
We get last digit by last digit of ${\,^{256}}{C_0}{10^0}{7^{256}}$
We divide of $256$ by $4$
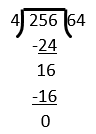
This number is divided completely, so
${7^0} = 1$
${I_1} = 1$
${I_2} = {\,^{256}}{C_1}{10^1}\,{7^{255}}$
$ = \dfrac{{256!}}{{256 - 1!1!}} \times {10^1} \times {7^{255}}$
$ = \dfrac{{256!}}{{255!1!}} \times {10^1} \times {7^{255}}$
$ = \dfrac{{256 \times 255!}}{{255!}} \times {10^1} \times {7^{255}}$
$ = 256 \times {10^1} \times {7^{253}}$
Now, we will complete the power of $255$
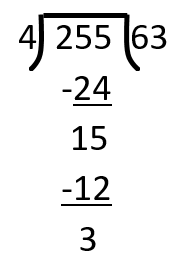
\[7 \times 7 \times 7 = 343\], we calculate last digit only
$6 \times 3 = 18$
Here last digit is also $8$
${17^{256}} = 81$
Note: Students should divide the powers of $17\,\,by\,\,4$. If the power is completely divided by $4$ then the answer will be given by ${7^4}$ and if the power is not completely divisible by $4$ then remainder will be left.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




