Question

How do you find the inverse of \[y = 2x - 5\] and graph them. Draw and label the line of symmetry for the inverse and the original graph.

Answer 1

Hint: Here in this question we have to find the inverse of the function, since the function is of the general form we use the concept of simple arithmetic operations and on further simplification we obtain the required solution for the given question. To find the inverse we swap the terms.

Complete step-by-step answer:
In mathematics, an inverse function is a function that "reverses" another function: if the function \[f\] applied to an input x gives a result of y, then applying its inverse function \[g\] to y gives the result x, i.e., \[g(y) = x\] if and only if \[f(x) = y\] . The inverse function of \[f\] is also denoted as \[{f^{ - 1}}\]
Now consider the given function \[y = 2x - 5\]
Now swap the variables that is y to x and x to y we have
 \[ \Rightarrow x = 2y - 5\]
Take 5 to LHS we get
 \[ \Rightarrow x + 5 = 2y\]
Divide the above equation by 2
 \[ \Rightarrow \dfrac{{x + 5}}{2} = y\]
Therefore it can be written as
 \[ \Rightarrow y = \dfrac{{x + 5}}{2}\]
Therefore the inverse of \[f(x) = 2x - 5\] is \[{f^{ - 1}}(x) = \dfrac{{x + 5}}{2}\]
we can verify by considering the example.
Consider \[f(x) = 2x - 5\] , now take x as 3. the value is \[f(3) = 2(3) - 5 = 6 - 5 = 1\]
Now consider \[{f^{ - 1}}(x) = \dfrac{{x + 5}}{2}\] , now take x as \[1\] then the value is \[{f^{ - 1}}\left( 1 \right) = \dfrac{{1 + 5}}{2} = \dfrac{6}{2} = 3\]
The graph for the given function and the inverse function is given below

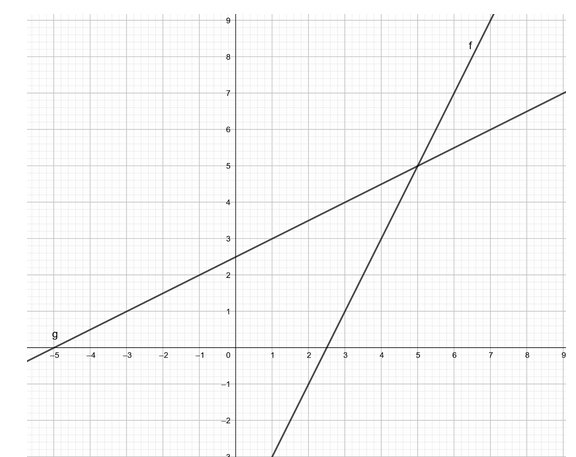
The lines of graphs are straight lines. therefore there is no line of symmetry.

Note: We must know about the simple arithmetic operations. To find the inverse we swap the y variable into x and simplify the equation and determine the value for y. since the solution we obtain will be in the form of fraction on simplification. While shifting the terms we must take care of signs.