Question

Find the intervals in which the function \[f\] given by \[f(x)=4{{x}^{3}}-6{{x}^{2}}-72x+30\] is (a) Strictly increasing (b) Strictly decreasing

Answer 1

Hint: We know that a defined function \[f(x)=4{{x}^{3}}-6{{x}^{2}}-72x+30\] is increasing in an interval if and only if the value of derivative in that interval is always positive; similarly it is decreasing in an interval if and only if the value of derivative in that interval is always negative. So we must the derivative of above function and write the sign of that expression in various intervals from where we guess the increasing and decreasing interval

Complete step-by-step answer:
We know that a relation is simply a set or collection of ordered pairs. An ordered pair, commonly known as a point, has two components which are the x and y coordinates, so any number of such ordered pairs taken in a set is called a relation. A function is actually a “special” kind of relation because it follows a few extra principles. Just like a relation, a function is also a set of ordered pairs; however, every x-value must be associated with a single y-value and for every value of x there must be a y value.

\[f(x)=4{{x}^{3}}-6{{x}^{2}}-72x+30\]

Now we differentiate the above function using formula given below,
\[y={{x}^{n}}\]
\[\dfrac{dy}{dx}=n{{x}^{n-1}}\]

Using above formula of differentiation of algebraic function, which is divide by plus/minus sign,

\[{f}'(x)=12{{x}^{2}}-12x+72\]

Now we take 12 as common from the function,

\[{f}'(x)=12({{x}^{2}}-x+6)\]

We now have to factorize the above equation,

\[{f}'(x)=12(x+2)(x-3)\]

Now, sign convention we write,

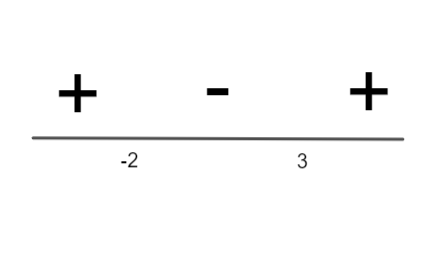
Hence, we find the interval in which function \[f\] is increasing, \[(-\infty ,-2)\cup (3,\infty )\] i.e. answer to (a) is \[(-\infty ,-2)\cup (3,\infty )\]
Hence, we find the interval in which function \[f\] is decreasing, \[(-2,3)\] i.e. answer to (b) is \[(-2,3)\]

Note: The student must be aware about the concept of derivative, Use of sign method in finding sign of function in that interval, and when a function is said to be increasing or decreasing. The common mistakes committed by students include wrong differentiation and performing wrong factorization of the differentiated function.