Question

How do you find the important points to graph \[f(x) = \dfrac{1}{{x - 3}}\]?

Answer 1

Hint: In the given equation, we are given an equation and we are asked to find the important points of the given equation. To get the y-intercept we will put x=0 and then to get the x-intercept we will put y=0. Since, we have the main points of the given equation, we can plot the required graph.

Complete step by step answer:
Given that, the function \[f(x) = \dfrac{1}{{x - 3}}\] we need to find the important points of the graph i.e. domain, range, standard form of the equation, non-defined points, etc.

First, we have to find the Domain of the function (\[{D_f}\]):
And for this, the denominator of the function should not become zero.
When the denominator of the function approaches 0, the function approaches infinity.
\[ \Rightarrow x - 3 \ne 0\]
\[ \Rightarrow x \ne 3\]

Here, \[{D_f}:x \in R - \{ 3\} \]
Thus, \[x \to 3 \Rightarrow f(x) \to \infty \]

Second, we should check the Range of the function (\[{R_f}\]):
Let, \[y = \dfrac{1}{{x - 3}}\]
\[ \Rightarrow yx - 3y = 1\]
\[ \Rightarrow yx = 1 + 3y\]
\[ \Rightarrow x = \dfrac{{1 + 3y}}{y}\]
Here, \[{R_f}:y \in R - \{ 0\} \]
Thus, \[y \to 0 \Rightarrow x \to \infty \]

Next, we should check for the standard form of equation:
Let, \[y = \dfrac{1}{{x - 3}}\]
\[ \Rightarrow yx - 3y = 1\]
\[ \Rightarrow yx = 1 + 3y\]
\[ \Rightarrow xy = 1 + 3y\]
It resembles \[xy = c\] which is the equation for the rectangular hyperbola.
Thus, this equation is in the standard form of rectangular hyperbola.

Also, we will find important points by finding the intercepts (both x and y).
(a) When \[x = 0\]

\[f(x) = \dfrac{1}{{x - 3}}\]

\[ \Rightarrow f(0) = \dfrac{1}{{0 - 3}}\]
\[ \Rightarrow f(0) = - \dfrac{1}{3}\]
Here, the y – intercept is \[0\].
Thus, the co-ordinates we get are \[(0, - \dfrac{1}{3})\].
(b) Let \[y = \dfrac{1}{{x - 3}}\]
When \[y = 0\]
\[ \Rightarrow 0 = \dfrac{1}{{x - 3}}\]
\[ \Rightarrow 0 = 1\] which is not possible.
This means, when $y=0$, $x$ value can’t be determined.
The graph of the function \[f(x) = \dfrac{1}{{x - 3}}\] will look like this:

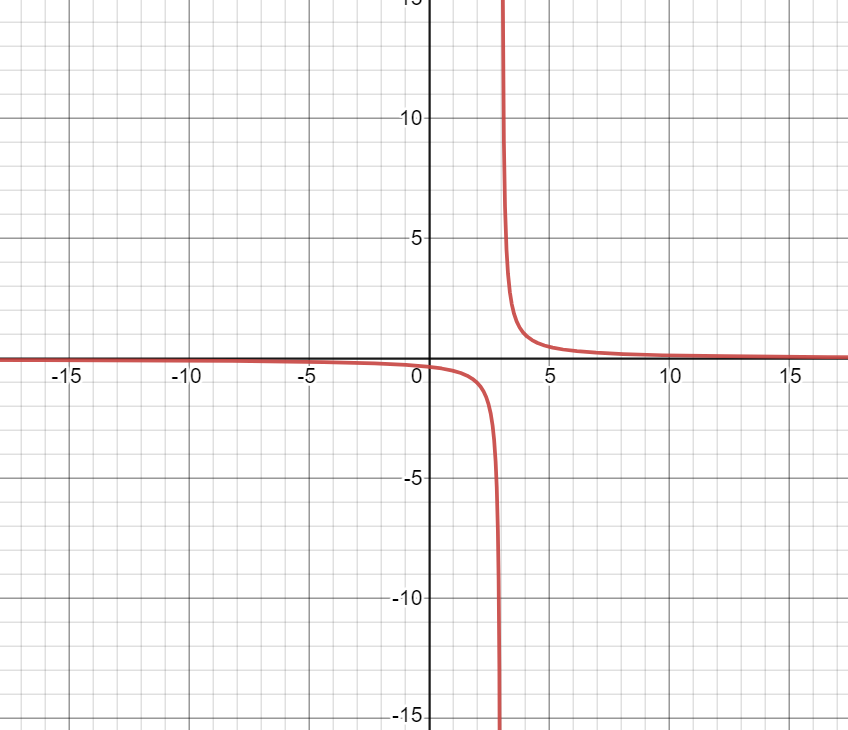
Note:
> In the above graph, when $y=0$, the value of $x$ seems to be approaching zero but it is not zero.
> The intercepts should be correctly known and accordingly only the graph will come out correctly. Also, the equation \[y = {x^2}\] gives the parabola which is open upwards. And, for the equation \[y = - {x^2}\] gives the parabola which is open downwards. We can find the vertex point by making the given equation in the form of the standard equation of the parabola.