Question

Find the image of the point (3,8) about the line x+3y = 7 assuming the line to be a plane mirror.

Answer 1

Hint: Assume the coordinates of the reflection point be B(x,y). Use the fact that the image distance is equal to object distance. Use the fact that the line joining object to the image is orthogonal to the reflecting surface. Hence form two equations in x and y. Solve for x and y. Hence find coordinates of B.
Alternatively, use the fact that the image of $A\left( {{x}_{1}},{{y}_{1}} \right)$ in the line mirror $ax+by+c=0$ is given by
$\dfrac{h-{{x}_{1}}}{a}=\dfrac{k-{{y}_{1}}}{b}=-2\dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{{{a}^{2}}+{{b}^{2}}}$, where h,k are the coordinates of the image.

Complete step-by-step solution -

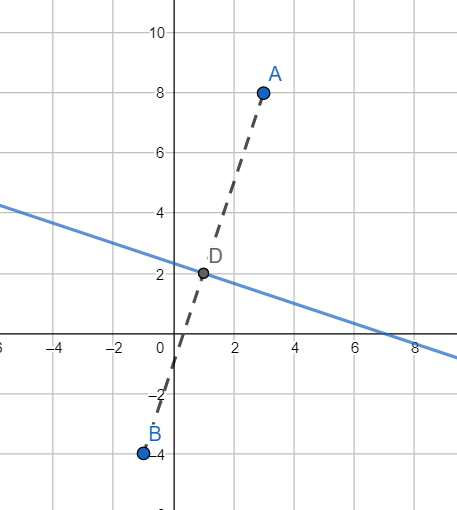
Let the coordinates of the image be B(x,y) and let the line AB intersect the line mirror at D.
Since image distance is equal to object distance, we have AD = DB
Hence $\dfrac{AD}{DB}=1$
Hence D is the midpoint of AB.
Now we know that coordinates of the midpoint of AB, where $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$, are given by
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{ y }_{2}}}{2} \right)$
Here ${{x}_{1}}=h,{{x}_{2}}=3,{{y}_{1}}=k$ and ${{y}_{2}}=8$
Hence $D\equiv \left( \dfrac{h+3}{2},\dfrac{k+8}{2} \right)$
Since D lies on the line mirror, we have
$\dfrac{h+3}{2}+3\left( \dfrac{k+8}{2} \right)=7\Rightarrow h+3k+13=0\text{ (i)}$.
Also, AB and the line mirror are perpendicular to each other.
Slope of AB $=\dfrac{k-8}{h-3}$
Slope of mirror $=\dfrac{-1}{3}$
We know that if the slopes of two perpendicular lines are ${{m}_{1}}$ and ${{m}_{2}}$ then ${{m}_{1}}{{m}_{2}}=-1$
Hence we have
$\begin{align}
  & \dfrac{k-8}{h-3}\left( \dfrac{-1}{3} \right)=-1 \\
 & \Rightarrow \dfrac{k-8}{h-3}=3 \\
 & \Rightarrow k=3h-1\text{ (ii)} \\
\end{align}$
Substituting the value of k from equation (ii) in equation (i), we get
$\begin{align}
  & h+3\left( 3h-1 \right)+13=0 \\
 & \Rightarrow 10h+10=0 \\
 & \Rightarrow h=-1 \\
\end{align}$
Substituting the value of h in equation (ii), we get
$k=3\left( -1 \right)-1=-4$
Hence the coordinates of the image are given by (-1,-4).

Note: Alternative Solution:
We know that the image of $A\left( {{x}_{1}},{{y}_{1}} \right)$ in the line mirror $ax+by+c=0$ is given by
$\dfrac{h-{{x}_{1}}}{a}=\dfrac{k-{{y}_{1}}}{b}=-2\dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{{{a}^{2}}+{{b}^{2}}}$, where h,k are the coordinates of the image.
Here $a=1,b=3,c=-7,{{x}_{1}}=3$ and ${{y}_{1}}=8$
Hence we have
$\begin{align}
  & \dfrac{h-3}{1}=\dfrac{k-8}{3}=-2\left( \dfrac{3+3\left( 8 \right)-7}{{{1}^{2}}+{{3}^{2}}} \right) \\
 & \Rightarrow h-3=\dfrac{k-8}{3}=-4 \\
\end{align}$
Hence $h=-4+3=-1$ and $k=8-12=-4$
Hence the coordinates of the image are given by
(-1,-4), which is the same as obtained above.