Question

Find the height of a building, when it is found that on walking toward it $ 40{\rm{ m}} $ in a horizontal line through its base the angular elevation of its top changes from $ 30^\circ $ to $ 45^\circ $ .

Answer 1

Hint: This question is based on Trigonometry. In this question we have to find the height of a building using the trigonometric relations. To solve this question, we first draw the diagram for this problem showing the height of the building and the angles that the person walking towards the building makes with the top of the building. Then using the trigonometric formula, we can calculate the height of the building.

Complete step-by-step answer:
Given:
Let us assume the height AB of the building is $ h $ metres.
Also, assuming the person is initially at point D on the ground and from this point the angle of the elevation to the top of the building is $ 30^\circ $ .
Now after moving $ CD = 40{\rm{ m}} $ towards the building the person reaches at point C on the ground and from this point the angle of the top of the building is $ 45^\circ $ .

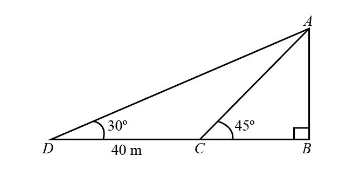
In $ \Delta ABC $ we have,
 $ \tan 45^\circ = \dfrac{{AB}}{{BC}} $
Since the value of $ \tan 45^\circ = 1 $ , so we get,
 $
\Rightarrow 1 = \dfrac{{AB}}{{BC}}\\
AB = BC
 $
We know that $ AB = h $
So, $ BC = h $

And similarly,
In $ \Delta ABD $ we have,
 $ \tan 30^\circ = \dfrac{{AB}}{{BD}} $
And from the figure we know that,
 $ BD = BC + CD $
We know that $ BC = h $ and $ CD = 40{\rm{ m}} $ , so we get,
 $ BD = h + 40 $
Substituting this value of BD in the formula we get,
 $ \Rightarrow \tan 30^\circ = \dfrac{h}{{h + 40}} $
Since the value of $ \tan 30^\circ = \dfrac{1}{{\sqrt 3 }} $ , so we get,
 $ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{h + 40}} $
Solving this equation for the value of $ h $ we get,
 $
\Rightarrow \sqrt 3 h = h + 40\\
\Rightarrow h\left( {\sqrt 3 - 1} \right) = 40\\
\Rightarrow h = \dfrac{{40}}{{\left( {1.732 - 1} \right)}}\\
\Rightarrow h = 54.64
 $
Therefore, the height of the building is $ 54.64{\rm{ m}} $ .

Note: It should be noted that when the angle of the elevation is given and we have to find either the height of the building or the distance from the building on the ground we always use the $ \tan \theta $ relationship formula, where $ \theta $ is the elevation angle.