
Find the greatest number of 5 digits exactly divisible by 12, 15 and 36. Find the smallest number which when increased by 20 is exactly divisible by 90 and 144 0. Find the smallest.
Answer
562.8k+ views
Hint: There are two parts of the questions. In the first part of the question, we have to find the greatest number of 5 digits which is exactly divisible by 12, 15 and 36. For that, we will find the L.C.M of these numbers. And then we will divide the greatest 5 digit number which is 99999 by the L.C.M obtained. We will subtract the remainder from the number 99999. Obtained numbers will be the greatest number of 5 digits which is divisible by 12, 15 and 36.
In the second part of the question, we have to find the smallest number which when increased by 20 is exactly divisible by 90 and 144. For that, we will find the L.C.M of 90 and 144. Then we will subtract 20 from the L.C.M to get the required number.
Complete step-by-step answer:
In the first part of the question, we have to find the greatest number of 5 digits exactly divisible by 12, 15 and 36. For that, we will find the L.C.M of 12, 15 and 36.
We know greatest 5-digit number $=99999$
First we will find all the factors of 12, 15 and 36.
$\begin{align}
& 12=2\times 2\times 3 \\
& 15=3\times 5 \\
& 36=3\times 3\times 2\times 2 \\
\end{align}$
The L.C.M of 12, 15 and 36 $=2\times 2\times 3\times 3\times 5=180$
Now, we will divide 99999 by 180 and we will find its remainder.
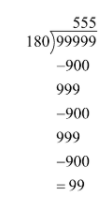
The remainder, which we have got after division of 99999 by 180, is 99.
Now, we will subtract the remainder from 99999.
$99999-99=99900$
Thus, the required number is 99900.
In the second part of the question, we have to find the smallest number which when increased by 20 is exactly divisible by 90 and 144.
First, we will find the L.C.M of 90 and 144.
We will find the factors of the 90 and 144.
$\begin{align}
& 90=2\times 3\times 3\times 5 \\
& 144=2\times 2\times 2\times 2\times 3\times 3 \\
\end{align}$
L.C.M of 90 and 144 $=2\times 2\times 2\times 2\times 3\times 3\times 5=720$
To get the required number, we will subtract 20 from 720.
So the required number is $=720-20=700$
Thus, the smallest number, which becomes exactly divisible by 90 and 144 after adding 20 to it $=700$
Note: Since we have calculated the L.C.M here, we need to know that term properly. L.C.M is a method to find the smallest common multiple of two or more numbers.
Some important properties of L.C.M are:-
L.C.M of any two or more numbers can’t be less than any of the numbers.
L.C.M of the co-prime numbers is equal to the product of the numbers, where co-prime number is the set of numbers which have only one as their common factor.
L.C.M of fractions is equal to the ratio of the L.C.M of the numerator to the H.C.F of the denominator.
In the second part of the question, we have to find the smallest number which when increased by 20 is exactly divisible by 90 and 144. For that, we will find the L.C.M of 90 and 144. Then we will subtract 20 from the L.C.M to get the required number.
Complete step-by-step answer:
In the first part of the question, we have to find the greatest number of 5 digits exactly divisible by 12, 15 and 36. For that, we will find the L.C.M of 12, 15 and 36.
We know greatest 5-digit number $=99999$
First we will find all the factors of 12, 15 and 36.
$\begin{align}
& 12=2\times 2\times 3 \\
& 15=3\times 5 \\
& 36=3\times 3\times 2\times 2 \\
\end{align}$
The L.C.M of 12, 15 and 36 $=2\times 2\times 3\times 3\times 5=180$
Now, we will divide 99999 by 180 and we will find its remainder.
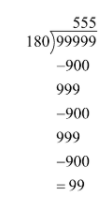
The remainder, which we have got after division of 99999 by 180, is 99.
Now, we will subtract the remainder from 99999.
$99999-99=99900$
Thus, the required number is 99900.
In the second part of the question, we have to find the smallest number which when increased by 20 is exactly divisible by 90 and 144.
First, we will find the L.C.M of 90 and 144.
We will find the factors of the 90 and 144.
$\begin{align}
& 90=2\times 3\times 3\times 5 \\
& 144=2\times 2\times 2\times 2\times 3\times 3 \\
\end{align}$
L.C.M of 90 and 144 $=2\times 2\times 2\times 2\times 3\times 3\times 5=720$
To get the required number, we will subtract 20 from 720.
So the required number is $=720-20=700$
Thus, the smallest number, which becomes exactly divisible by 90 and 144 after adding 20 to it $=700$
Note: Since we have calculated the L.C.M here, we need to know that term properly. L.C.M is a method to find the smallest common multiple of two or more numbers.
Some important properties of L.C.M are:-
L.C.M of any two or more numbers can’t be less than any of the numbers.
L.C.M of the co-prime numbers is equal to the product of the numbers, where co-prime number is the set of numbers which have only one as their common factor.
L.C.M of fractions is equal to the ratio of the L.C.M of the numerator to the H.C.F of the denominator.
Recently Updated Pages
Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Convert 200 Million dollars in rupees class 7 maths CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

Repeated addition of the same number is called a addition class 7 maths CBSE





