Question

Find the following ratio.
$\tan x$, \[\cos \left( {{90}^{\circ }}-y \right)\] , $\sin y$, \[\cos \left( {{90}^{\circ }}-x \right)\], \[\tan \left( {{90}^{\circ }}-x \right)\] , $\sin x$

Answer 1

Hint: To solve this question, we will use the trigonometric formulas given as \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}},\cos \theta =\dfrac{\text{base}}{\text{hypotenuse}},\sin \theta =\dfrac{\text{perpendicular}}{\text{hypotenuse}}.\] To solve this, we will consider triangle BAD and triangle ADC separately and then apply these above stated formulas to get the result.

Complete step-by-step solution:
Consider the triangle given below.

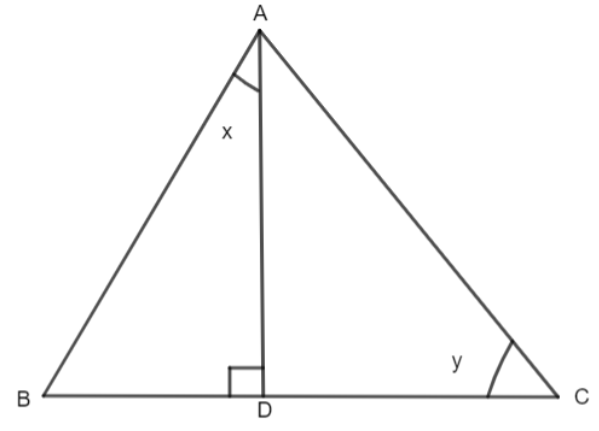
We have to calculate tan x first by using the formula of \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] in a triangle. In triangle BAD, we have,
\[\tan x=\dfrac{\text{perpendicular}}{\text{base}}\]
In triangle BAD, here perpendicular is BD and the base is AD. Therefore, we get,
\[\Rightarrow \tan x=\dfrac{BD}{AD}......\left( i \right)\]
Now to compute \[\cos \left( {{90}^{\circ }}-y \right)\], consider triangle ADC given,
\[\angle ACD=y\]
\[\angle ACD={{90}^{\circ }}\]
Then by angle sum property of the triangle, we have the sum of all three angles of the triangle as \[{{180}^{\circ }}.\]
\[\Rightarrow \angle ADC+\angle ACD+\angle DAC={{180}^{\circ }}\]
\[\Rightarrow {{90}^{\circ }}+y+\angle DAC={{180}^{\circ }}\]
\[\Rightarrow \angle DAC={{180}^{\circ }}-{{90}^{\circ }}-y\]
\[\Rightarrow \angle DAC={{90}^{\circ }}-y\]
So, we have in triangle ADC, \[\angle DAC={{90}^{\circ }}-y.\]
Now, \[\cos \theta =\dfrac{\text{base}}{\text{hypotenuse}}\] where \[\theta \] is an angle in the given triangle.
In triangle ADC, AC is the hypotenuse and AD is the base with respect to angle DAC.
\[\cos \left( \angle DAC \right)=\dfrac{\text{base}}{\text{hypotenuse}}\]
\[\Rightarrow \cos \left( \angle DAC \right)=\dfrac{AD}{AC}\]
\[\angle DAC={{90}^{\circ }}-y\]
\[\Rightarrow \cos \left( {{90}^{\circ }}-y \right)=\dfrac{AD}{AC}.....\left( ii \right)\]
Now to compute sin y, use the formula of \[\sin \theta \] given as \[\sin \theta =\dfrac{\text{perpendicular}}{\text{hypotenuse}}.\]
In triangle ADC,
\[\sin y=\dfrac{\text{perpendicular}}{\text{hypotenuse}}\]
Here, perpendicular is AD and hypotenuse is AC.
\[\Rightarrow \sin y=\dfrac{AD}{AC}.....\left( iii \right)\]
Now, consider triangle ABD,
\[\angle BAD=x\]
\[\angle ADB ={{90}^{\circ }}\]
As by linearity, ADC is a straight line and \[\angle ADC={{90}^{\circ }},\] then by angle sum property of the triangle stated above, we have,
\[\angle ADB+\angle ABD+\angle DAB={{180}^{\circ }}\]
\[\Rightarrow {{90}^{\circ }}+x+\angle ABD={{180}^{\circ }}\]
\[\Rightarrow \angle ABD={{180}^{\circ }}-{{90}^{\circ }}-x\]
\[\Rightarrow \angle ABD={{90}^{\circ }}-x\]
Now, in triangle ABD,
\[\cos \left( \angle ABD \right)=\dfrac{\text{base}}{\text{hypotenuse}}\]
\[\Rightarrow \cos \left( \angle ABD \right)=\dfrac{BD}{AB}\]
Now, as \[\angle ABD={{90}^{\circ }}-x\]
\[\Rightarrow \cos \left( {{90}^{\circ }}-x \right)=\dfrac{BD}{AB}......\left( iv \right)\]
Again the same triangle ABD,
\[\tan \left( {{90}^{\circ }}-x \right)=\dfrac{\text{perpendicular}}{\text{base}}\]
\[\Rightarrow \tan \left( {{90}^{\circ }}-x \right)=\dfrac{AD}{BD}.....\left( v \right)\]
Finally, we have to compute sin x. Consider triangle ABD,
\[\sin x=\dfrac{\text{perpendiuclar}}{\text{hypotenuse}}\]
\[\Rightarrow \sin x=\dfrac{BD}{AB}.....\left( vi \right)\]
From equations (i), (ii), (iii), (iv), (v) and (vi), we have our answers as
\[\tan x=\dfrac{BD}{AD}\]
\[\cos \left( {{90}^{\circ }}-y \right)=\dfrac{AD}{AC}\]
\[\sin y=\dfrac{AD}{AC}\]
\[\cos \left( {{90}^{\circ }}-x \right)=\dfrac{BD}{AB}\]
\[\tan \left( {{90}^{\circ }}-x \right)=\dfrac{AD}{BD}\]
\[\sin x=\dfrac{BD}{AB}\]

Note: Another method to compute \[\cos \left( {{90}^{\circ }}-y \right)\] is by using the formula \[\cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta .\] Replace \[\theta \] by y we have, so we get, \[\sin y=\dfrac{AD}{AC}.\]
\[\Rightarrow \cos \left( {{90}^{\circ }}-y \right)=\sin y=\dfrac{AD}{AC}\]
\[\Rightarrow \cos \left( {{90}^{\circ }}-y \right)=\dfrac{AD}{AC}\]
Similarly, we can compute \[\cos \left( {{90}^{\circ }}-x \right)\] from sin x by using \[\cos \left( {{90}^{\circ }}-x \right)=\sin x.\]