Question

Find the focal distance of the point on the respective parabola: \[{y^2} = 16x\] . Given that: ordinate is twice the length of abscissa.
(a) \[\pi \]
(b) \[7\]
(c) \[8\]
(d) \[5\]

Answer 1

Hint: The given problem revolves around the concepts of curved equations like parabola, hyperbola, eclipse, etc. So, we will first analyze the given equation with the general formulae \[{y^2} = 4ax\] of parabola. Then, by using the given conditions, substituting it in the equation and using the focal distance of parabola, the desired solution can be obtained with the help of distance formula respectively.

Complete step-by-step answer:
Since, we have given the parabolic equation i.e.
 \[{y^2} = 16x\]
 $ \because $ We know that,
The generalized formula or an equation to represent parabola is,
 \[ \Rightarrow {y^2} = 4ax\]

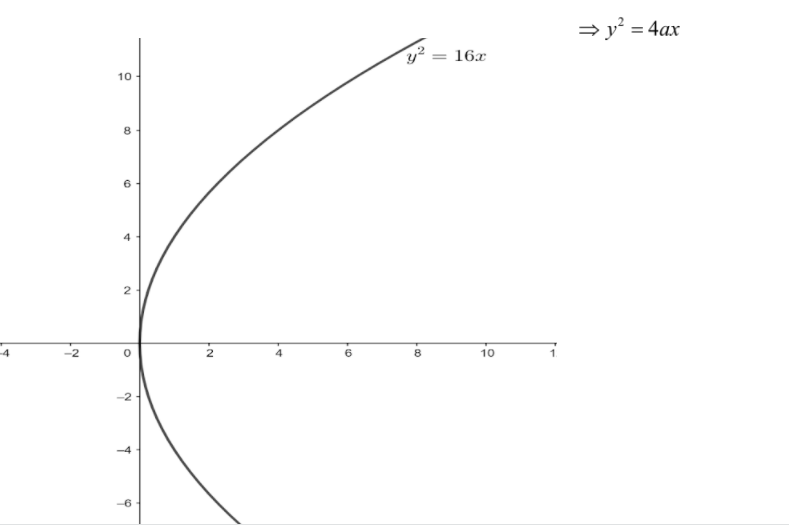
As a result, comparing the given parabolic equation to the above standardized equation of parabola, we get
 \[
   \Rightarrow {y^2} = 4ax = 16x \\
  \therefore 4ax = 16x \;
 \]
Solving the equation mathematically, we get
 \[
   \Rightarrow 4a = 16 \\
   \Rightarrow a = 4 \;
 \]
But, we have given the condition that,
Ordinate (i.e. y-coordinate) is twice than that of abscissa (i.e. x-coordinate) that is $ y = 2x $ ,
The equation becomes,
 \[
   \Rightarrow {\left( {2x} \right)^2} = 16x \\
  \therefore 4{x^2} = 16x \;
 \]
Solving the equation mathematically (to find the exact coordinates), we get
 \[
  \therefore 4{x^2} - 16x = 0 \\
   \Rightarrow 4x\left( {x - 4} \right) = 0 \;
 \]
As the equation is quadratic, it may have two possible values, we get,
 \[ \Rightarrow 4x = 0\] Or \[x - 4 = 0\]
 $ \therefore x = 0 $ Or $ x = 4 $ … (i)
Hence, y-coordinate becomes,
 \[ \Rightarrow y = 2x = 0\] Or \[y = 2x = 8\]
 $ \because $ We also know that,
Focal distance of parabola is represented by $ x + a $ respectively
Hence, the required solution is about to overcome that
When $ x = 0 $ ,
 \[
   \Rightarrow f{\text{ocal distance}} = x + a \\
  \therefore f{\text{ocal distance}} = 0 + 4 = 4 \;
 \] … (ii)
Similarly, when $ x = 4 $ , we get
 \[
   \Rightarrow f{\text{ocal distance}} = x + a \\
  \therefore f{\text{ocal distance}} = 4 + 4 = 8 \;
 \] … (iii)
By using distance formula \[x = \sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2}} \] , we get
From (i), (ii) and (iii) respectively,
 \[
  \therefore x = \sqrt {{{\left( {4 - 4} \right)}^2} + {{\left( {8 - 0} \right)}^2}} \\
  \therefore x = \sqrt {0 + 64} = 8 \;
 \]
 $ \Rightarrow \therefore $ The option (c) is correct!
So, the correct answer is “Option C”.

Note: One must know able to compare the given equation of curve with respect to curve being asked to solve, here the curve is parabola which is represented by $ {y^2} = 4ax $ and its respective parameter like focal length $ x + a $ , etc. In any geometry of the problem distance formula \[x = \sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2}} \] so as to be sure of our final answer.