Question

Find the flux through the disc.

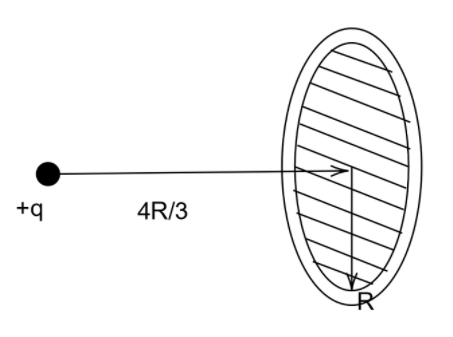
Answer 1

Hint: We are asked to find the flux through the given disc. We have to redraw the diagram first. Then we can move onto finding the solid angle with respect to the charge. Once we have done that, we can find the flux through the disc by equating it with the value of one standard value. Thus, leading us to the required solution.
Formulas used: The standard value of steradian is taken as \[4\pi steradian \to \dfrac{9}{{{\varepsilon _0}}}\]
Here, the arrow indicates “corresponds to”

Complete answer:
Let us start by redrawing the diagram so that we can find the solid angle value easily. Here we construct a triangle in order to get a clear and more helpful understanding of the solid angle in discussion. The unit of solid angle is called a steradian which is denoted by the small letters “sr”
Redrawing the diagram, we have

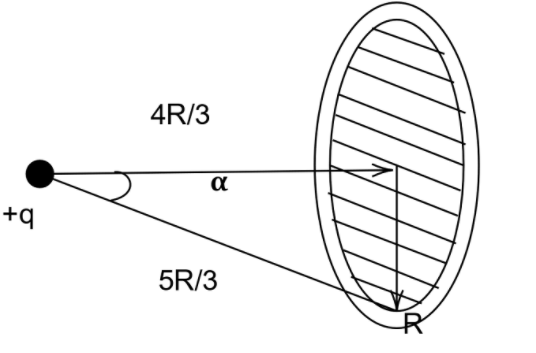
The solid angle here is \[\theta = 2\pi \left( {1 - \cos \alpha } \right)\]
Now from the triangle in the figure, we can find the value of cosine alpha and get
\[\theta = 2\pi \left( {1 - \cos \alpha } \right) \Rightarrow 2\pi \left( {1 - \dfrac{4}{5}} \right) = \dfrac{{2\pi }}{5}\]
Now we can use the standard value of the solid angle and equate the two together. That is,
\[4\pi steradian \to \dfrac{9}{{{\varepsilon _0}}}\]
\[\dfrac{{2\pi }}{5} \to x\]
Cross multiplying the two equations we get,
\[x = \dfrac{{\dfrac{{2\pi }}{5} \times \dfrac{9}{{{\varepsilon _0}}}}}{{4\pi sr}}\]
After cancellation and further simplification, we get \[x = \dfrac{9}{{10{\varepsilon _0}}}\]

Note:
Flux is defined as the amount of electric flux passing through a given space or surface. It is also a way of describing how strong the electric field is. In short, flux is a measure of how strong the electric field is. It gives us an idea about the electric field intensity and strength.