Question

Find the exact value of \[\operatorname{cosec} \theta \] trigonometric functions for the angle formed when the terminal side passes through \[\left( {3,4} \right)\].
A. \[\dfrac{4}{5}\]
B. \[\dfrac{3}{5}\]
C. \[\dfrac{5}{3}\]
D. \[\dfrac{5}{4}\]

Answer 1

Hint: The terminal side is the one that can be anywhere and defines the angle. As the terminal side passes through \[\left( {3,4} \right)\] we have indirectly given the lengths of opposite side and adjacent side. By using Pythagoras theorem, find the hypotenuse and then the value of \[\operatorname{cosec} \theta \].

Complete step-by-step answer:

The angle formed by the terminal side passes through \[\left( {3,4} \right)\] is shown in the below figure:

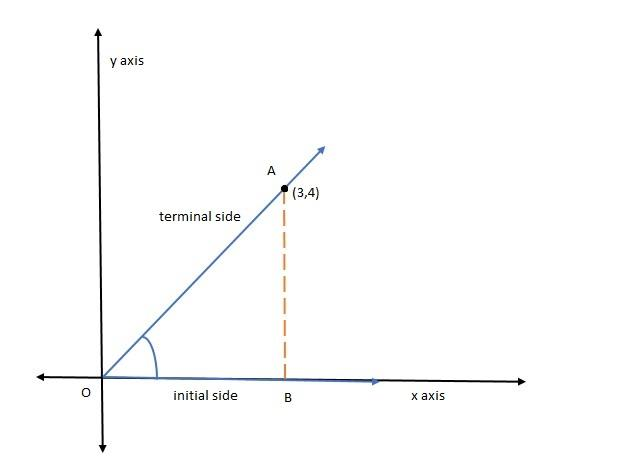
Where \[\angle AOB = \theta \]

Clearly from the figure,

\[
  AB = 4{\text{ units }}\left( {{\text{Opposite side}}} \right) \\
  OB = 3{\text{ units }}\left( {{\text{Adjacent side}}} \right) \\
\]

Using Pythagoras theorem i.e., \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left(
{{\text{Opposite}}} \right)^2} + {\left( {{\text{Adjacent}}} \right)^2}\], we have

\[

  {\left( {OA} \right)^2} = {\left( {AB} \right)^2} + {\left( {OB} \right)^2} \\

  {\left( {OA} \right)^2} = {\left( 4 \right)^2} + {\left( 3 \right)^2} \\

  {\left( {OA} \right)^2} = 16 + 9 = 25 \\

  \therefore OA = 5 \\

\]

We know that \[\operatorname{cosec} \theta =
\dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite side}}}}\].

Thus, we have \[\operatorname{cosec} \theta = \dfrac{5}{3}\]

Therefore, the correct option is C. \[\dfrac{5}{3}\]

Note: Pythagoras theorem states that \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Opposite}}} \right)^2} + {\left( {{\text{Adjacent}}} \right)^2}\]. Also remember that the initial side is a stationary straight line that contains a point about which another straight line is rotated to form an angle.