Question

How do you find the exact value of $\arctan (2)$?

Answer 1

Hint: $\arctan (2)$ cannot be represented as a rational number of degrees or as a rational multiple of $\pi$radians. We need to represent $\arctan (2)$ as a sum of an infinite series. $\arctan (x) = \sum\limits_{k = 0}^\infty {{{( - 1)}^k}\dfrac{{{x^{2k + 1}}}}{{2k + 1}}}$.

Complete Step by Step Solution:
Consider the following right-angled triangle

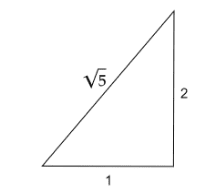
These sides of the triangle for $\arctan (2)$ are as follows:
Opposite = 2, Adjacent = 1, and Hypotenuse = $\sqrt 5$
However, $\arctan (2)$ cannot be represented as a rational number of degrees or as a rational multiple of radians.
Therefore, we need a different method to represent this. Hence, we represent $\arctan (2)$ as a sum of an infinite series.
$\arctan (x)$can be represented as
$\Rightarrow \arctan (x)=\sum\limits_{k=0}^{\infty }{{{(-1)}^{k}}\dfrac{{{x}^{2k+1}}}{2k+1}=x-\dfrac{{{x}^{3}}}{3}+\dfrac{{{x}^{5}}}{5}-\dfrac{{{x}^{7}}}{7}+\dfrac{{{x}^{9}}}{9}-\dfrac{{{x}^{11}}}{11}+...}$
This, however, can only be converged for $|x| \leqslant 1$
In order for this series to converge, we need to use:
$\Rightarrow \tan \left( \dfrac{\pi }{2}-x \right)=\dfrac{1}{\tan x}$
Taking arctan on both sides of the equation, we get
$\Rightarrow \arctan \left( \dfrac{1}{x} \right)=\dfrac{\pi }{2}-\arctan \left( x \right)$
Substituting the values of x in the above equation,
$\Rightarrow \arctan (2)=\dfrac{\pi }{2}-\arctan \left( \dfrac{1}{2} \right)$
Simplifying the equation, we arrive at the conclusion,

$\Rightarrow \arctan (2)=\dfrac{\pi }{2}-\sum\limits_{k=0}^{\infty }{{{(-1)}^{k}}\dfrac{1}{{{2}^{2k+1}}(2k+1)}}$

Note:
Every trigonometric function has an inverse function. The inverse function works in a reverse manner. An inverse function is written with an arc in front of the name of the function, i.e., arcsine, arccos, arctan, etc. $\arctan (x)$ implies an angle whose tangent is equal to x.
$\tan \left( {60^\circ } \right) = 1.732$ which implies the tangent of $60^\circ$ is 1.732
$\arctan (1.732) = 60^\circ$ which implies the angle whose tangent is 1.732 is
Trigonometric functions can be applied to any angle including large and obtuse angles. However, inverse functions pose a problem because we will find many angles having the same tangent. For example, $45{}^\circ$ and $\left( 360+45 \right){}^\circ$ will have the same tangent. In order to solve this problem, the range of solutions of inverse functions is limited so that we get only one result for each input value.