Question

Find the equations of the sides of a triangle whose vertices are at A (-1, 8), B (4, -2) and C (-5, -3).

Answer 1

Hint: Every side of a triangle has two endpoints or vertices. A line is drawn through these points to make a side. Here the points are given in the question we just have to find the equation of the line through these points using two points form of an equation

Complete step-by-step answer:
Two points form of a linear equation is $ y - {y_1} = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)\left( {x - {x_1}} \right) $ where the first point is $ \left( {{x_1},{y_1}} \right) $ and $ \left( {{x_2},{y_2}} \right) $ is the second point.
We are given a triangle with vertices A (-1, 8), B (4, -2) and C (-5, -3).

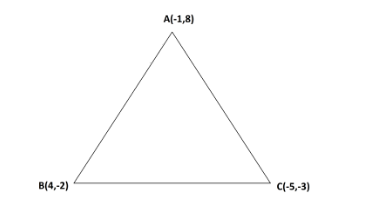
We have to find the equations of the sides of the above triangle ABC.
Equation when two points are given is $ y - {y_1} = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)\left( {x - {x_1}} \right) $
Equation of side AB= $ y - {y_1} = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)\left( {x - {x_1}} \right) $
Where $
  \left( {{x_1},{y_1}} \right) = A( - 1,8) = ( - 1,8) \\
  \left( {{x_2},{y_2}} \right) = B(4, - 2) = (4, - 2) \\
 $
  $
  y - 8 = \left( {\dfrac{{ - 2 - 8}}{{4 - \left( { - 1} \right)}}} \right)\left( {x - \left( { - 1} \right)} \right) \\
  y - 8 = \left( {\dfrac{{ - 10}}{{4 + 1}}} \right)\left( {x + 1} \right) \\
  y - 8 = \left( {\dfrac{{ - 10}}{5}} \right)\left( {x + 1} \right) \\
  y - 8 = \left( { - 2} \right)\left( {x + 1} \right) \\
  y - 8 = - 2x - 2 \\
  2x + y - 8 + 2 = 0 \\
  2x + y - 6 = 0 \\
 $
Equation of side AB is $ 2x + y - 6 = 0 $
Equation of side BC= $ y - {y_1} = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)\left( {x - {x_1}} \right) $
Where $
  \left( {{x_1},{y_1}} \right) = B(4, - 2) = (4, - 2) \\
  \left( {{x_2},{y_2}} \right) = C( - 5, - 3) = ( - 5, - 3) \\
 $
  $
  y - \left( { - 2} \right) = \left( {\dfrac{{ - 3 - \left( { - 2} \right)}}{{ - 5 - 4}}} \right)\left( {x - 4} \right) \\
  y + 2 = \left( {\dfrac{{ - 3 + 2}}{{ - 9}}} \right)\left( {x - 4} \right) \\
  y + 2 = \left( {\dfrac{{ - 1}}{{ - 9}}} \right)\left( {x - 4} \right) \\
  y + 2 = \left( {\dfrac{1}{9}} \right)\left( {x - 4} \right) \\
  9\left( {y + 2} \right) = x - 4 \\
  9y + 18 = x - 4 \\
  x - 9y - 4 - 18 = 0 \\
  x - 9y - 22 = 0 \\
 $
Equation of side BC is $ x - 9y - 22 = 0 $
Equation of side CA= $ y - {y_1} = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)\left( {x - {x_1}} \right) $
Where $
  \left( {{x_1},{y_1}} \right) = C( - 5, - 3) = ( - 5, - 3) \\
  \left( {{x_2},{y_2}} \right) = A( - 1,8) = ( - 1,8) \\
 $
   $
  y - \left( { - 3} \right) = \left( {\dfrac{{8 - \left( { - 3} \right)}}{{ - 1 - \left( { - 5} \right)}}} \right)\left( {x - \left( { - 5} \right)} \right) \\
  y + 3 = \left( {\dfrac{{8 + 3}}{{ - 1 + 5}}} \right)\left( {x + 5} \right) \\
  y + 3 = \left( {\dfrac{{11}}{4}} \right)\left( {x + 5} \right) \\
  y + 3 = \left( {\dfrac{{11}}{4}} \right)\left( {x + 5} \right) \\
  4\left( {y + 3} \right) = 11\left( {x + 5} \right) \\
  4y + 12 = 11x + 55 \\
  11x - 4y + 55 - 12 = 0 \\
  11x - 4y + 43 = 0 \\
 $
Equation of side CA is $ 11x - 4y + 43 = 0 $
Equations of sides AB, BC, CA are $ 2x + y - 6 = 0 $ , \[x - 9y - 22 = 0\], \[11x - 4y + 43 = 0 $ respectively.

Note: To form a line we at least need two points. A line is defined as a line of points that extends infinitely in two directions. It has one dimension, length. Points that are on the same line are called collinear points. A line is written with an arrowhead.