Question

Find the equations of tangent and normal to the curve $x=a{{\sin }^{3}}\theta $ and $y=a{{\cos }^{3}}\theta $ at \[\theta =\dfrac{\pi }{4}\].

Answer 1

Hint: To solve this problem, we should know the concept related to the tangent and normal to a curve at a point. We should know that the slope of tangent at a point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the curve $y=f\left( x \right)$ is given by $m={{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$. We know that the normal is perpendicular to the tangent, the slope of normal can be given by the formula ${{m}_{normal}}={{\left. -\dfrac{dx}{dy} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$. In the question, we are not given a direct function in x and y. Instead we are given x and y in terms of a parameter $\theta $. Then we can rearrange the slope of tangent as $m={{\left. \dfrac{\dfrac{dy}{d\theta }}{\dfrac{dx}{d\theta }} \right|}_{\left( {{\theta }_{1}} \right)}}$. Using this relation and the parametric equations, we can find the slope of the tangent and normal. We also have the x and y coordinates of the point and using the slope and the point, we can get the equation of the tangent and the normal. The equation of a line with slope m and coordinates of the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.

Complete step by step answer:
We are given the parametric equations of the curve as $x=a{{\sin }^{3}}\theta $ and $y=a{{\cos }^{3}}\theta $.
We are asked to find the equations of tangent and normal to the curve at \[\theta =\dfrac{\pi }{4}\].
We know the relation between the slopes of tangent and normal and the equation of the curve.
The slope of tangent at a point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the curve $y=f\left( x \right)$ is given by $m={{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$. We know that the normal is perpendicular to the tangent, the slope of normal can be given by the formula ${{m}_{normal}}={{\left. -\dfrac{dx}{dy} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$
In the question, we are not given a direct function in x and y. Instead we are given x and y in terms of a parameter $\theta $. Then we can rearrange the slope of tangent as $m={{\left. \dfrac{\dfrac{dy}{d\theta }}{\dfrac{dx}{d\theta }} \right|}_{\left( {{\theta }_{1}} \right)}}$.
Calculating the values of $\dfrac{dx}{d\theta }$ and $\dfrac{dy}{d\theta }$ at \[\theta =\dfrac{\pi }{4}\]
\[\begin{align}
  & x=a{{\sin }^{3}}\theta \\
 & \dfrac{dx}{d\theta }=3a{{\sin }^{2}}\theta \cos \theta \\
 & {{\left. \dfrac{dx}{d\theta } \right|}_{\theta =\dfrac{\pi }{4}}}=3a{{\sin }^{2}}\left( \dfrac{\pi }{4} \right)\cos \left( \dfrac{\pi }{4} \right)=3a{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}\left( \dfrac{1}{\sqrt{2}} \right)=\dfrac{3a}{2\sqrt{2}} \\
\end{align}\]
\[\begin{align}
  & y=a{{\cos }^{3}}\theta \\
 & \dfrac{dy}{d\theta }=3a{{\cos }^{2}}\theta \left( -\sin \theta \right) \\
 & {{\left. \dfrac{dy}{d\theta } \right|}_{\theta =\dfrac{\pi }{4}}}=-3a{{\cos }^{2}}\left( \dfrac{\pi }{4} \right)\sin \left( \dfrac{\pi }{4} \right)=-3a{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}\left( \dfrac{1}{\sqrt{2}} \right)=-\dfrac{3a}{2\sqrt{2}} \\
\end{align}\]
From the relation $m={{\left. \dfrac{\dfrac{dy}{d\theta }}{\dfrac{dx}{d\theta }} \right|}_{\left( {{\theta }_{1}} \right)}}$
We get the slope of the tangent as $m={{\left. \dfrac{\dfrac{dy}{d\theta }}{\dfrac{dx}{d\theta }} \right|}_{\left( \dfrac{\pi }{4} \right)}}=\dfrac{\dfrac{-3a}{2\sqrt{2}}}{\dfrac{3a}{2\sqrt{2}}}=-1$
We know that the tangent and normal are perpendicular to each other. We know that the product of slopes of perpendicular lines is -1. Using this, we get the slope of normal as
$\begin{align}
  & {{m}_{normal}}\times -1=-1 \\
 & {{m}_{normal}}=1 \\
\end{align}$
At \[\theta =\dfrac{\pi }{4}\] the x and y coordinates are
$\begin{align}
  & x=a{{\sin }^{3}}\dfrac{\pi }{4}=\dfrac{a}{2\sqrt{2}} \\
 & y=a{{\cos }^{3}}\dfrac{\pi }{4}=\dfrac{a}{2\sqrt{2}} \\
\end{align}$
The equation of a line with slope m and coordinates of the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
Equation of tangent with slope = -1 is
$\begin{align}
  & y-\dfrac{a}{2\sqrt{2}}=-1\left( x-\dfrac{a}{2\sqrt{2}} \right) \\
 & y-\dfrac{a}{2\sqrt{2}}=-x+\dfrac{a}{2\sqrt{2}} \\
 & x+y=\dfrac{a}{2\sqrt{2}}+\dfrac{a}{2\sqrt{2}}=\dfrac{a}{\sqrt{2}} \\
 & x+y=\dfrac{a}{\sqrt{2}} \\
\end{align}$
Equation of normal with slope = 1 is
\[\begin{align}
  & y-\dfrac{a}{2\sqrt{2}}=\left( x-\dfrac{a}{2\sqrt{2}} \right) \\
 & y-\dfrac{a}{2\sqrt{2}}=x-\dfrac{a}{2\sqrt{2}} \\
 & y=x \\
 & x-y=0 \\
\end{align}\]

$\therefore $ The equations of tangent and normal are $x+y=\dfrac{a}{\sqrt{2}}$ and \[x-y=0\] respectively.

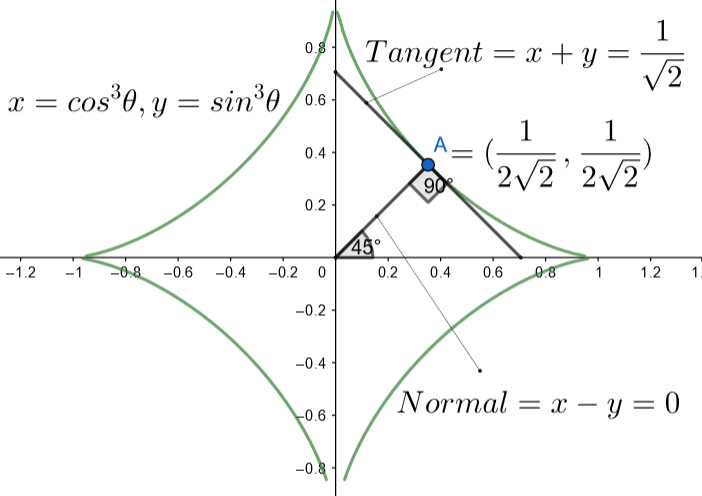
The above graph is a curve in the family of the curves in the question when a = 1.

Note: Students who don’t know how to arrange the term $\dfrac{dy}{dx}$ in terms of the parameter can remove the parameter from the process. That is
$\begin{align}
  & \dfrac{x}{a}={{\sin }^{3}}\theta ,\dfrac{y}{a}={{\cos }^{3}}\theta \\
 & {{\left( \dfrac{x}{a} \right)}^{\dfrac{1}{3}}}=\sin \theta ,{{\left( \dfrac{y}{a} \right)}^{\dfrac{1}{3}}}=\cos \theta \\
 & {{\left( {{\left( \dfrac{x}{a} \right)}^{\dfrac{1}{3}}} \right)}^{2}}+{{\left( {{\left( \dfrac{y}{a} \right)}^{\dfrac{1}{3}}} \right)}^{2}}={{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\
 & {{\left( \dfrac{x}{a} \right)}^{\dfrac{2}{3}}}+{{\left( \dfrac{y}{a} \right)}^{\dfrac{2}{3}}}=1 \\
 & {{x}^{\dfrac{2}{3}}}+{{y}^{\dfrac{2}{3}}}={{a}^{\dfrac{2}{3}}} \\
\end{align}$
Now, we can apply the usual process to find the equations of tangent and normal.