
Find the equation of the perpendicular bisector of the line joining the points (1,3) and (3,1).
Answer
621.9k+ views
Hint: First of all, try to represent the given conditions of the question in the form of a figure. Then with the help of the figure, evaluate the equations of the line and the other information by using the given values.
Complete step-by-step answer:
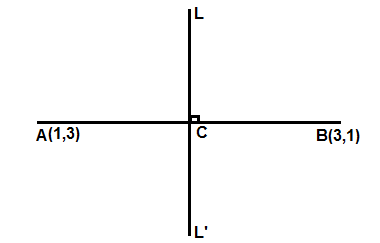
Let us assume a line AB with endpoints A (1,3) and B (3,1). Let C be the mid-point such that the line LL’ passing through the point C is at right angle with the line AB.
The coordinates of the mid-point C can be calculated as
$ = \left( {\left( {\dfrac{{1 + 3}}{2}} \right),\left( {\dfrac{{3 + 1}}{2}} \right)} \right)$
$ = \left( {\left( {\dfrac{4}{2}} \right),\left( {\dfrac{4}{2}} \right)} \right)$
$ = \left( {2,2} \right)$
Now, we know that the LL’ is perpendicular to the line AB.
Also, we know that if two lines are perpendicular, the product of their slope is equal to -1.
Therefore, by using the above condition, we get
${m_{LL'}}{m_{AB}} = - 1$ … (1)
We have the formula for calculating the slope of the equation as
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ … (2)
Now by using the above given formula, we can calculate the slope of the line AB
${m_{AB}} = \dfrac{{1 - 3}}{{3 - 1}}$
$\therefore {m_{AB}} = - 1$ … (3)
After substituting the value of slope from equation (3) in the equation (1), we get
${m_{LL'}}( - 1) = - 1$
$\therefore {m_{LL'}} = 1$ … (4)
Now, the equation of a line can be written as
$y - {y_1} = m(x - {x_1})$ … (5)
So, the equation of the line LL’ can be written as
$y - 2 = 1(x - 2)$
$ \Rightarrow y - 2 = x - 2$
$\therefore x - y = 0$
Hence, the required equation of the line is $x - y = 0$.
Note: The students can be mistaken in finding the equations of the line as the various formulas are used to reach this equation, like slope is needed to be calculated first, sometimes the coordinates are also calculated. So, the students need an adequate knowledge of these concepts before proceeding for these solutions.
Complete step-by-step answer:
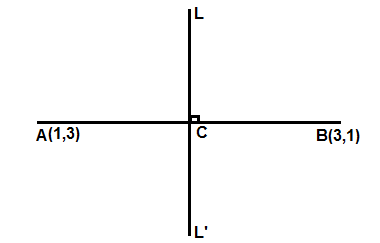
Let us assume a line AB with endpoints A (1,3) and B (3,1). Let C be the mid-point such that the line LL’ passing through the point C is at right angle with the line AB.
The coordinates of the mid-point C can be calculated as
$ = \left( {\left( {\dfrac{{1 + 3}}{2}} \right),\left( {\dfrac{{3 + 1}}{2}} \right)} \right)$
$ = \left( {\left( {\dfrac{4}{2}} \right),\left( {\dfrac{4}{2}} \right)} \right)$
$ = \left( {2,2} \right)$
Now, we know that the LL’ is perpendicular to the line AB.
Also, we know that if two lines are perpendicular, the product of their slope is equal to -1.
Therefore, by using the above condition, we get
${m_{LL'}}{m_{AB}} = - 1$ … (1)
We have the formula for calculating the slope of the equation as
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ … (2)
Now by using the above given formula, we can calculate the slope of the line AB
${m_{AB}} = \dfrac{{1 - 3}}{{3 - 1}}$
$\therefore {m_{AB}} = - 1$ … (3)
After substituting the value of slope from equation (3) in the equation (1), we get
${m_{LL'}}( - 1) = - 1$
$\therefore {m_{LL'}} = 1$ … (4)
Now, the equation of a line can be written as
$y - {y_1} = m(x - {x_1})$ … (5)
So, the equation of the line LL’ can be written as
$y - 2 = 1(x - 2)$
$ \Rightarrow y - 2 = x - 2$
$\therefore x - y = 0$
Hence, the required equation of the line is $x - y = 0$.
Note: The students can be mistaken in finding the equations of the line as the various formulas are used to reach this equation, like slope is needed to be calculated first, sometimes the coordinates are also calculated. So, the students need an adequate knowledge of these concepts before proceeding for these solutions.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

Draw the diagram of the sectional view of the human class 10 biology CBSE




