Question

Find the equation of the parabola whose directrix makes an isosceles right angled triangle of area 4 square units with axes in ${{3}^{rd}}$ quadrant and focus is on the line $y=x$, 2 units away from the origin.

Answer 1

Hint: Draw a diagram of the given situation and find the equation of the directrix using the information given about the area of the isosceles right angled triangle. Now find the coordinates of focus of the parabola by assuming the coordinates as $\left( x,x \right)$ and applying the distance formula. Finally, assume a point $\left( h,k \right)$ on the parabola and use the relation$\text{Eccentricity of a parabola=}\dfrac{\text{distance of the point on the parabola from focus}}{\text{distance of the point on the parabola from directrix}}$
And equate it equal to 1 to get the equation of parabola in terms of $\left( h,k \right)$. Replace $\left( h,k \right)$ with $\left( x,y \right)$ to get the final equation.

Complete answer:
Let us draw a diagram of the given conditions in the question.

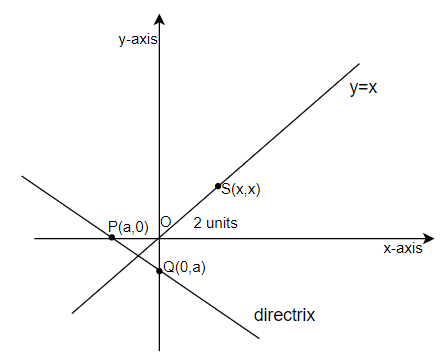
In the above figure, we have assumed a directrix which is making a right - angled isosceles triangle POQ with the axes in the third quadrant. The directrix is assumed to meet the x and y-axis at $P\left( a,0 \right)$ and $Q\left( 0,a \right)$ respectively. We have also assumed a focus $S\left( x,x \right)$ on the line $y=x$ which is at a distance 2 units from the origin, that is OS = 2 units.
Now, since the area of $\Delta POQ$ is 4 square units, therefore applying the formula for the area of a right angle triangle, we have,
$\begin{align}
  & Ar.\left( \Delta PQO \right)=4 \\
 & \Rightarrow \dfrac{1}{2}\times base\times height=4 \\
 & \Rightarrow \dfrac{1}{2}\times OQ\times OP=4 \\
 & \Rightarrow \dfrac{1}{2}\times a\times a=4 \\
 & \Rightarrow {{a}^{2}}=8 \\
 & \Rightarrow a=\pm 2\sqrt{2}\text{ }units \\
\end{align}$
Since, point a is in the third quadrant, therefore it must be negative for both x and y. So, we have $a=-2\sqrt{2}$. Hence, the points are $P\left( -2\sqrt{2},0 \right)$ and $Q\left( 0,-2\sqrt{2} \right)$. So, the equation of the directrix can be given as $y=mx+c$, where m is the slope and c is the intercept on y-axis. Clearly, we can see that the slope is -1 and the y-intercept is $-2\sqrt{2}$. Therefore, the equation of the directrix is given as :
$\begin{align}
  & y=-x+\left( -2\sqrt{2} \right) \\
 & \Rightarrow x+y+2\sqrt{2}=0 \\
\end{align}$
Now, let us come to the information about the focus of the parabola. It is given that the distance of focus from the origin is 2 units.
$\Rightarrow OS=2\text{ }units$
So, applying the distance formula given as $\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ by assuming $O\left( 0,0 \right)as\left( {{x}_{1}},{{y}_{1}} \right)$ and $S\left( x,x \right)as\left( {{x}_{2}},{{y}_{2}} \right)$, we get,
$\begin{align}
  & \Rightarrow \sqrt{{{\left( 0-x \right)}^{2}}+{{\left( 0-x \right)}^{2}}}=2 \\
 & \Rightarrow \sqrt{{{x}^{2}}+{{x}^{2}}}=2 \\
 & \Rightarrow \sqrt{2{{x}^{2}}}=2 \\
 & \Rightarrow \sqrt{2}x=2 \\
 & \Rightarrow x=\sqrt{2} \\
\end{align}$
Hence, point S is given by the coordinate $\left( \sqrt{2},\sqrt{2} \right)$.
Now, to find the locus or equation of the parabola, we assume any point $\left( h,k \right)$ on it. We know that eccentricity of a parabola is 1 and it is the ratio of distance of point on the parabola from focus to the distance of point on the parabola from the directrix.

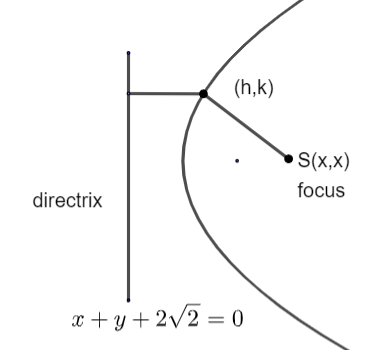
$\text{Eccentricity = }\dfrac{\text{distance of }\left( h,k \right)\text{ from }S\left( \sqrt{2},\sqrt{2} \right)}{\text{distance of }\left( h,k \right)\text{ from }x+y+2\sqrt{2}=0}=1$
So, applying the distance formula in the numerator and the formula to determine the distance of a point $\left( \alpha ,\beta \right)$ from a line $ax+by+c$ given as $\left| \dfrac{a\alpha +b\beta +c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ in the denominator, we get,
$\begin{align}
  & \Rightarrow \dfrac{\sqrt{{{\left( h-\sqrt{2} \right)}^{2}}+{{\left( k-\sqrt{2} \right)}^{2}}}}{\left| \dfrac{h+k+2\sqrt{2}}{\sqrt{{{1}^{2}}+{{1}^{2}}}} \right|}=1 \\
 & \Rightarrow \sqrt{2}\times \sqrt{{{\left( h-\sqrt{2} \right)}^{2}}+{{\left( k-\sqrt{2} \right)}^{2}}}=\left| h+k+2\sqrt{2} \right| \\
\end{align}$
On squaring both sides we get,
$\Rightarrow 2\times \left[ {{\left( h-\sqrt{2} \right)}^{2}}+{{\left( k-\sqrt{2} \right)}^{2}} \right]={{\left( h+k+2\sqrt{2} \right)}^{2}}$
Applying the formula ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ in the L.H.S and ${{\left( a+b+c \right)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca$ in the R.H.S, we get,$\Rightarrow 2\times \left[ {{h}^{2}}+2-2\sqrt{2}h+{{k}^{2}}+2-2\sqrt{2}k \right]={{h}^{2}}+{{k}^{2}}+8+2kh+4\sqrt{2}h+4\sqrt{2}k$
On simplification, we get,
$\Rightarrow {{h}^{2}}+{{k}^{2}}-8\sqrt{2}h-8\sqrt{2}k-2hk=0$
Now, replacing $\left( h,k \right)$ with $\left( x,y \right)$, we get,
\[~\Rightarrow {{x}^{2}}+{{y}^{2}}-2xy-8\sqrt{2}x-8\sqrt{2}y=0\]
The above expression is the required equation of parabola.

Note:
One may note that it is necessary to draw the graph of the given situation so that we can visualize the situation better and do not get confused. You must know the distance formula and properties of parabola to solve the above question. You may note that we have assumed the focus (S) of the parabola as $\left( x,x \right)$. This is because it lies on the line $y=x$ and therefore, abscissa and ordinate must be equal.